Поскольку коэффициент К представляет некоторый практический интерес, то во многих справочниках вместо Y и s приводятся У и К. Но если вам нужно знать а, то вы всегда можете получить это значение из формулы (38.9). Из этой формулы видно также, что коэффициент Пуассона s должен быть меньше 1/ 2. Если бы это было не так, то объемный модуль К был бы отрицательным и материал при увеличении давления расширялся бы. Это позволило бы добывать механическую энергию из любого кубика, т. е. это означало бы, что кубик находится в неустойчивом равновесии. Если бы он начал расширяться, то расширение продолжалось бы само по себе с высвобождением энергии.
Посмотрим, что получится, если мы приложим к чему-то «косое» напряжение. Под косым, или скалывающим, напряжением мы подразумеваем такое воздействие, как показано на фиг. 38.4.
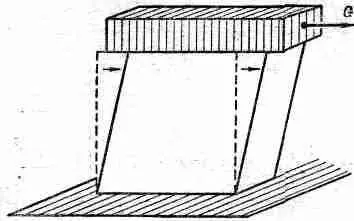
Фиг. 38.4. Однородный сдвиг.
В качестве предварительной задачи посмотрим, какова будет деформация кубика под действием сил, показанных на фиг. 38.5.
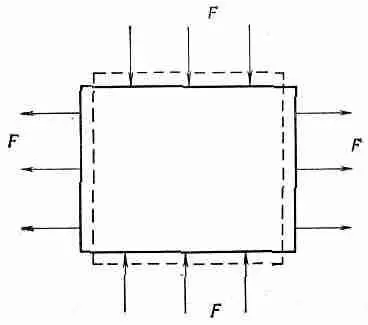
Фиг. 38.5. Действие сжимающих сил, давящих на вершину и основание, и равных им растягивающих сил с двух сторон.
Снова можно разделить эту задачу на две: вертикальное давление и горизонтальное растяжение. Обозначая через А площадь грани кубика, мы получаем для изменения горизонтальной длины
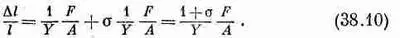
Изменение же высоты по вертикали равно просто тому же выражению с обратным знаком.
Предположим теперь, что мы имеем тот же самый кубик, и подвергнем его действию сдвиговых сил, показанных на фиг. 38.6, а.
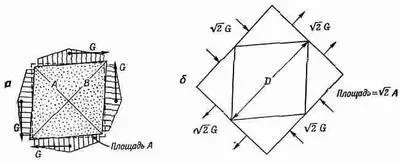
Фиг. 38.6. Две пары сил сдвига (а) создают то же самое напряжение, что и сжимающие = растягивающие силы (б).
Заметим теперь, что все силы должны быть равными, ибо на тело не должен действовать никакой момент сил и оно должно находиться в равновесии. (Подобные силы должны действовать также и в случае, изображенном на фиг. 38.4, поскольку кубик находится в равновесии. Они обеспечиваются тем, что кубик «приклеен» к столу.) При таких условиях говорят, что кубик находится в состоянии чистого сдвига. Но обратите внимание, что если мы разрежем кубик плоскостями под углом 45°, скажем, вдоль диагонали А на фиг. 38.6, а, то полная сила, действующая в этой плоскости, нормальна к ней и равна Ц2G.Площадь, на которой действует эта сила, равна Ц2A;следовательно, напряжение, нормальное к этой плоскости, будет просто G/A. Точно так же если взять плоскость, наклоненную под углом 45° в другую сторону, т. е. по диагонали В, то мы увидим, что на ней действует нормальное сдавливающее напряжение, равное - G/A. Из этого ясно, что напряжение при «чистом сжатии» эквивалентно комбинации растягивающего и сжимающего напряжений, направленных под прямым углом друг к другу и под углом 45° к первоначальным граням кубика. Внутренние напряжения и деформации будут такими же, как и в большом кубике материала под действием сил, показанных на фиг. 38.6, б. Но эту задачу мы уже решили. Изменение длины диагонали задается уравнением (38.10):

(Одна диагональ сокращается, а другая удлиняется.)
Часто деформацию сдвига удобно описывать с помощью угла «искажения» кубика q, показанного на фиг. 38.7.
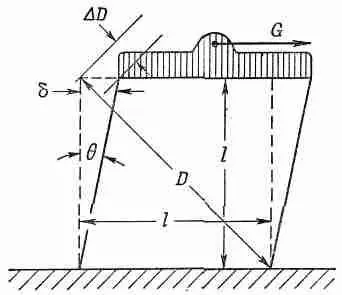
Фиг. 38.7. Напряжение сдвига q равно 2DD/D.
Из геометрии фигуры вы видите, что горизонтальный сдвиг б верхнего края равен Ц 2DD, так что
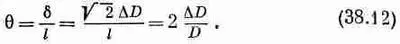
Напряжение сдвига g определяется как отношение тангенциальной силы, действующей на грань, к площади грани g=G/A. Воспользовавшись уравнением (38.11), мы из (38.12) получаем
Читать дальше



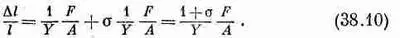






![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
