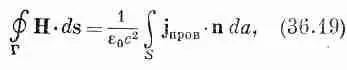
где интеграл от jберется по поверхности S, ограниченной контуром Г. Каждый виток обмотки пересекает эту поверхность один раз, поэтому каждый виток дает в интеграл вклад, равный I , а поскольку всего витков N штук, то интеграл будет равен NI. Из симметрии нашей задачи видно, что В одинаково на всем контуре Г, если, конечно, намагниченность, а следовательно, и поле Нтоже постоянны на контуре Г. Уравнение (36.19) при таких условиях принимает вид
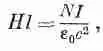
где l —длина кривой Г. Таким образом,

Именно из-за того что в задачах подобного типа поле Нпрямо пропорционально намагничивающему току, оно иногда называется намагничивающим.
Единственное, что нам теперь требуется,— это уравнение, связывающее Нс В. Однако такого уравнения просто не существует! У нас есть, конечно, уравнение (36.18), но от него мало проку, ибо в ферромагнитных материалах типа железа оно не дает прямой связи между Ми В. Намагниченность М зависит от всей предыдущей истории данного образца железа, а не только от того, каково поле В в данный момент и как оно изменялось раньше.
Впрочем, еще не все потеряно. В некоторых простых случаях мы все же можем найти решение. Если взять ненамагниченное железо, скажем, отожженное при высокой температуре, то для такого простого тела, как тор, магнитная предыстория всего железа будет одной и той же. Затем из экспериментальных измерений мы можем кое-что сказать относительно М, а следовательно, и о связи между Ви Н. Из уравнения (36.20) видно, что поле Ввнутри тора равно произведению некоторой постоянной на величину тока в обмотке I. А поле Вможно измерить интегрированием по времени э.д.с. в намагничивающей обмотке, изображенной на рисунке (или в дополнительной обмотке, намотанной поверх нее). Эта э.д.с. равна скорости изменения потока В, так что интеграл от э.д.с. по времени равен произведению Вна площадь поперечного сечения тора.
На фиг. 36.8 показано соотношение между Ви Н, наблюдаемое в сердечнике из мягкого железа.
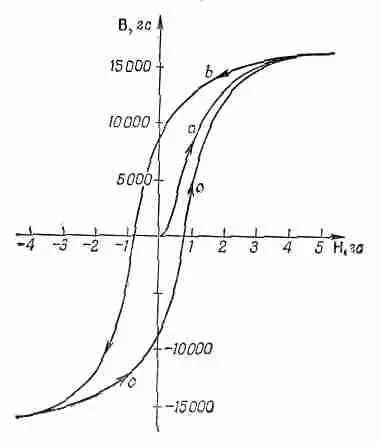
Фиг. 36.8. Типичная кривая намагничивания и петля гистерезиса мягкого железа.
Когда ток включается в первый раз, увеличение Вс Нпроисходит по кривой а. Обратите внимание на различие масштабов по осям Ви Н; вначале, чтобы получить большое В, необходимо относительно малое Н. Почему же в случае железа поле В намного больше, чем было бы без него? Да потому, что возникает большая намагниченность М, эквивалентная большому поверхностному току в железе, а поле определяется суммой этого тока и тока проводимости в обмотке. А почему намагниченность Моказывается такой большой, мы обсудим позднее.
При больших значениях Нкривая намагничивания «выравнивается». Мы говорим, что железо насыщается. В масштабах нашей фигуры кривая становится горизонтальной, на самом же деле намагниченность продолжает слабо расти: для больших полей Встановится равным Ни намагниченность Муже не увеличивается. Кстати, если бы сердечник был сделан из немагнитного материала, то намагниченность Мбыла бы равна нулю, а В было бы равно для всех полей Н.
Прежде всего заметим, что кривая а на фиг. 36.8, так называемая кривая намагничивания,— в высшей степени нелинейна. Впрочем, положение здесь гораздо сложнее. Если после достижения насыщения мы уменьшим ток в катушке и вернем Нснова к нулю, магнитное поле В будет падать по кривой b. Когда Ндостигнет нуля, В еще не будет нулем. Даже после выключения намагничивающего тока магнитное поле в железе остается: железо становится постоянно намагниченным. Если теперь включить в катушке ток в обратном направлении, то кривая В— Нпойдет дальше по ветви b до тех пор, пока железо не намагнитится до насыщения в противоположном направлении. При дальнейшем уменьшении тока до нуля В пойдет по кривой с. Когда мы меняем ток от большой положительной до большой отрицательной величины, кривая В— Нбудет идти вверх и вниз очень близко к ветвям b и c . Если же, однако, Нменять каким-то произвольным образом, то возникнут более сложные кривые, которые, вообще говоря, будут лежать между кривыми b и c . Кривая, полученная повторными изменениями полей, называется петлей гистерезиса.
Читать дальше

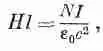





![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
