откуда, вспоминая, что площадь равна ас, получаем
I=М z b.
Другими словами, на каждой из вертикальных поверхностей величина тока на единицу длины по вертикали равна М z .
Представьте теперь два таких маленьких кубика, расположенных рядом друг с другом (фиг. 36.5).
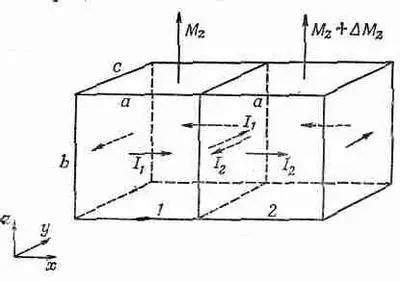
Фиг. 36.5. Если намагниченность двух соседних кубиков различна, то на их границе течет поверхностный ток.
Кубик 2 несколько смещен по отношению к кубику 1, поэтому его вертикальная компонента намагниченности будет немного другой, скажем M z+DМ z. Теперь полный ток на поверхности между этими двумя кубиками будет слагаться из двух частей. По кубику 1 в положительном направлении по оси у течет ток I 1, а по кубику 2 в отрицательном направлении течет ток I 2. Полный поверхностный ток в положительном направлении оси у будет равен сумме
I=I 1-I 2= М z b-(М z +D М z) b =-DM zb.
Величину D М г можно записать в виде произведения производной от M z по х на смещение кубика 2 относительно кубика 1, которое как раз равно а:
DM z=( д M z/ д x)а. Тогда ток, текущий между двумя кубиками, будет равен
I=(- д M z/ д x)ab.
Чтобы связать ток I со средней объемной плотностью тока j, необходимо понять, что этот ток на самом деле размазан по некоторой области поперечного сечения. Если мы вообразим, что такими маленькими кубиками заполнен весь объем материала, то за такое сечение (перпендикулярное оси х) может быть выбрана боковая грань одного из кубиков. Теперь вы видите, что площадь, связанная с током, как раз равна площади ab одной из фронтальных граней. В результате получаем
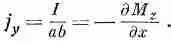
Наконец-то у нас начинает получаться ротор М.
Но в выражении для j y должно быть еще одно слагаемое, связанное с изменением x-компоненты намагниченности с изменением z. Этот вклад в jпроисходит от поверхности между двумя маленькими кубиками, поставленными друг на друга (фиг. 36.6).
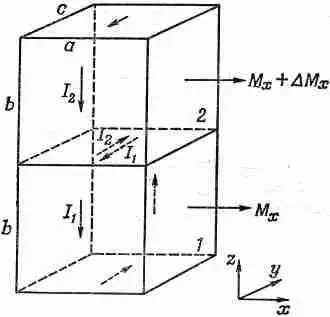
Фиг. 36.6. Два кубика, расположенных один над другим, тоже могут давать вклад в j y .
Воспользовавшись только что проведенными рассуждениями, мы можем показать, что эта поверхность будет давать в величину j yвклад, равный dM x /dz. Только эти поверхности и будут давать вклад в y-компоненту тока, так что полная плотность тока в направлении оси у получается равной
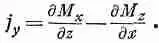
Определяя токи на остальных гранях куба или используя тот факт, что направление оси z было выбрано совершенно произвольно, мы можем прийти к заключению, что вектор плотности тока действительно определяется выражением .
j= СX M.
Итак, если вы решили описывать магнитное состояние вещества через средний магнитный момент единицы объема М, то оказывается, что циркулирующие атомные токи эквивалентны средней плотности тока в веществе, определяемой выражением (36.7). Если же материал обладает вдобавок еще диэлектрическими свойствами, то в нем может возникнуть и поляризационный ток j пол =d P /dt. А если материал к тому же и проводник, то в нем может течь и ток проводимости j пров. Таким образом, полный ток можно записать как
J = J пр o в+ СXM+ д P / д t; (36.10)
§ 2. Поле Н
Теперь можно подставить выражение для тока (36.10) в уравнение Максвелла. Мы получаем
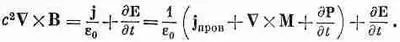
Слагаемое с Мможно перенести в левую часть: 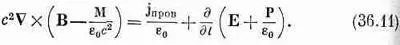
Как мы уже отмечали в гл. 32, иногда удобно записывать ( Е+ Р/e 0) как новое векторное поле D/e 0. Точно так же удобно ( В-М/e 0с 2) записывать в виде единого векторного поля. Такое поле мы обозначим через Н, т. е.
Читать дальше




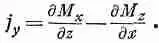
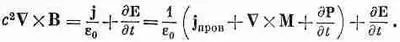
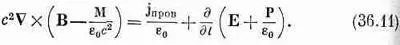



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
