Ричард Фейнман - 7. Физика сплошных сред

Поле В в зазоре будет по величине тем же самым. Это следу­ет из уравнений (36.16). Представьте себе замкнутую поверх­ность S (см. фиг. 36.11,б), одна грань которой находится в зазоре, а другая — в железе. Полный поток поля В через эту поверхность должен быть равен нулю. Обозначая через В 1 величину поля в зазоре, а через B 2— величину поля в железе, мы видим, что

B 1 A 1 -В 2 А 2 =0,

а поскольку А 1 =А 2 , то отсюда следует, что В 1 =В 2 .

Посмотрим теперь на Н. Мы снова можем воспользоваться уравнением (36.19), взяв криволинейный интеграл по контуру Г (см. фиг. 36.11,6). Как и прежде, правая часть равна NI — произведению числа витков на ток. Однако теперь Н в железе и в воздухе будет различным. Обозначая через Н 2 поле в железе, а через l 2— Длину пути по окружности ярма, мы видим, что эта часть кривой дает вклад в интеграл H 2 l 2 . Если же поле в зазоре равно Н 1 , а ширина его l 1 , то вклад зазора оказывается равным H 1 l 1 . Таким образом, получаем

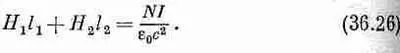
Но это еще не все. Нам известно еще, что намагниченность в воздушной щели пренебрежимо мала, так что B 1 =H 1 . А так как B 1=B 2, то уравнение (36.26) принимает вид

Остаются еще два неизвестных. Чтобы найти В 2 и H 2 , необхо­димо еще одно соотношение, которое связывает В с H в железе.

Если можно приближенно считать, что B 2=mH 2, то уравнение разрешается алгебраически. Рассмотрим более общий случай, для которого кривая намагничивания железа имеет вид, изоб­раженный на фиг. 36.8. Единственное, что нам нужно,— это найти совместное решение этого функционального соотношения с уравнением (36.27). Его можно найти, строя зависимость (36.27) на одном графике с кривой намагничивания, как это сделано на фиг. 36.12. Точки, где эти кривые пересекутся, и будут нашими решениями.

Для данного тока I уравнение (36.27) описывается прямой линией, обозначенной I >0 на фиг. 36.12. Эта линия пересекает ось Н (B 2=0) в точке H 2 =NI/e 0 c 2 l 2 и имеет наклон - l 2 /l 1 Различные величины токов приводят просто к горизонтальному сдвигу этой линии. Из фиг. 36.12 мы видим, что при данном токе существует нес­колько различных решений, зависящих от того, каким об­разом вы получили их.

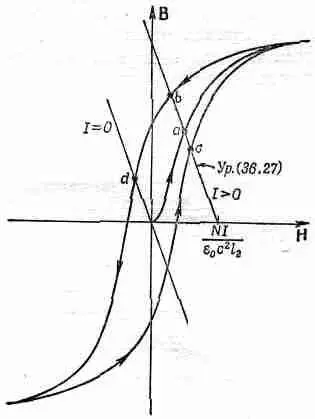
Фиг. 36.12. Определение поля в электромагните.

Если вы только что построили маг­нит и включили ток /, то поле B 2(которое равно B 1) будет иметь величину, определяе­мую точкой а. Если вы сначала увеличили ток до очень большой величины, а затем пони­зили до I , то значение поля будет определяться точкой b. А если, увеличивая ток от большого отрицательного значения, вы до­шли до /, то поле определяется точкой с. Поле в зазоре зависит от того, как вы поступали в прошлом.

Если ток в магните равен нулю, то соотношение между В 2 и H 2 в уравнении (36.27) изображается кривой, обозначенной I =0 на фиг. 36.12. Здесь опять возможны различные решения. Если вы первоначально «насытили» железо, то в магните может сохраниться значительное остаточное поле, определяемое точ­кой d. Вы можете снять обмотку и получить постоянный маг­нит. Нетрудно понять, что для хорошего постоянного магнита необходим материал с широкой петлей гистерезиса. Такую очень широкую петлю имеют специальные сплавы, подобные Алнико V.

§ 6. Спонтанная намагниченность

Обратимся теперь к вопросу, почему в ферромагнитных мате­риалах даже малые магнитные поля приводят к такой большой намагниченности. Намагниченность ферромагнитных материа­лов типа железа или никеля образуется благодаря магнитным моментам электронов одной из внутренних оболочек атома. Магнитный момент m каждого электрона равен произведению q/2m на g-фактор и момент количества движения J. Для отдель­ного электрона при отсутствии чисто орбитального движения g=2, а компонента Jв любом направлении, скажем, в направ­лении оси z, равна ±h/2, так что компонента m в направлении оси z будет