Статистическая механика говорит нам, что вероятность нахождения атома в каком-то состоянии пропорциональна
g - (энергия состояния)/ kT .
В отсутствие магнитного поля энергия обоих состояний одна и та же, поэтому в случае равновесия в магнитном поле вероятности пропорциональны
е - D U / kT , (35.14)
Число же атомов в единице объема со спином, направленным вверх, равно

а со спином, направленным вниз,

Постоянная а должна определяться из условия
N вверх+N вниз=N (35.17)
т.е. равна полному числу атомов в единице объема. Таким образом, мы получаем
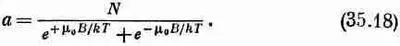
Однако нас интересует средний магнитный момент в направлении оси z. Каждый атом со спином, направленным вверх, дает в этот момент вклад, равный -m 0, а со спином, направленным вниз, + m 0, так что средний момент будет
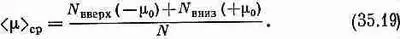
Тогда М — магнитный момент единицы объема — будет равен N ср. Воспользовавшись выражениями (35.15)—(35.17), получим
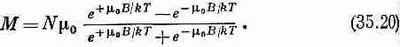
Это и есть квантовомеханическая формула для М в случае атомов со спином j= 1/ 2. К счастью, ее можно записать более коротко через гиперболический тангенс:

График зависимости М он В приведен на фиг. 35.7.
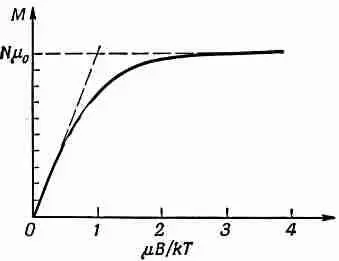
Фиг. 35.7. Изменение намагниченности парамагнетика при изменении напряженности магнитного поля В .
Когда поле В становится очень большим, гиперболический тангенс приближается к единице, а М — к своему предельному значению Nm 0. Таким образом, при сильных полях происходит насыщение. Нетрудно понять, почему так получается — ведь при достаточно больших полях все магнитные моменты выстраиваются в одном и том же направлении. Другими словами, при насыщении все атомы находятся в состоянии со спинами, направленными вниз, и каждый из них дает вклад в магнитный момент, равный m 0.
Обычно при комнатной температуре и полях, которые можно получить (порядка 10000 гс), отношение m 0 B/kT равно приблизительно 0,02. Чтобы наблюдать насыщение, необходимо спуститься до очень низких температур. Для комнатной и более высоких температур обычно можно thx заменить на x и написать

Точно так же, как и в классической теории, намагниченность М оказывается пропорциональной полю В. Даже формула оказывается той же самой, за исключением того, что в ней, по-видимому, где-то потерян множитель 1 / 3 . Но нам еще нужно связать m 0 в квантовомеханической формуле с величиной m , которая появилась в классическом результате, в выражении (35.9).
В классической формуле у нас появилось m 2 =m·m— квадрат вектора магнитного момента, или
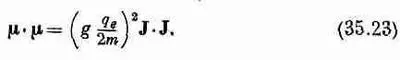
В предыдущей главе я уже говорил, что очень часто правильный ответ можно получить из классических вычислений с заменой J·Jна j (j+1)h 2 . В нашем частном примере j= 1/ 2, так что
j(j+1)h 2= 3/ 4h 2.
Подставляя этот результат вместо J·Jв (35.23), получаем
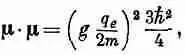
или, вводя величину m 0 , определенную соотношением (35.12), получаем
m·m=3m 2 0.
Читать дальше



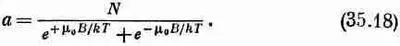
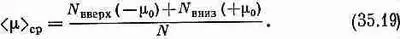
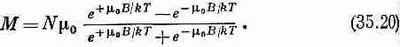



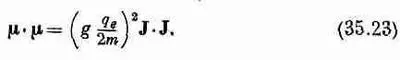
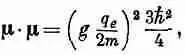



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
