Ричард Фейнман - 7. Физика сплошных сред

Интересно, что к такому же заключению можно прийти и с классической точки зрения. В соответствии с классической картиной, когда мы помещаем гироскоп, обладающий магнит­ным моментом m, и моментом количества движения 3, во внешнее магнитное поле, гироскоп начнет прецессировать вокруг оси, параллельной этому полю (фиг. 35.3).

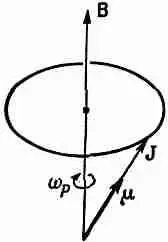
Фиг. 35.3. Классическая прецессия атома с магнитным моментом m и моментом количества движения J ,

Предположим, нас инте­ресует, как можно изменить угол классического гироскопа по отношению к магнитному полю, т. е. по отношению к оси z? Магнитное поле создает момент силы относительно горизон­тальной оси. На первый взгляд кажется, что такой момент силы старается выстроить магниты в направлении поля, но он вызывает только прецессию. Если же мы хотим изменить угол гироскопа по отношению к оси z, то должны приложить момент силы относительно оси z. Если мы приложим момент силы, действующий в том же направлении, что и прецессия, угол гироскопа изменится и это приведет к уменьшению компоненты Jв направлении оси z. Угол между направлением Jи осью z на фиг. 35.3 должен увеличиться. Если мы попытаемся воспре­пятствовать прецессии, вектор Jбудет двигаться по направле­нию к вертикали.

Но каким образом к наше­му прецессирующему атому можно приложить нужный момент силы? Ответ: с по­мощью слабого магнитного поля, направленного в сто­рону. На первый взгляд вам может показаться, что нап­равление этого магнитного поля должно крутиться вмес­те с прецессией магнитного момента, так чтобы поле всегда было направлено к нему под прямым углом, как это показано на фиг. 35.4, а с помощью поля В'.

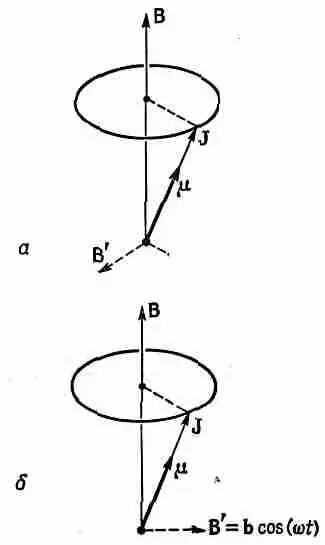
Фиг. 35.4. Угол прецессии атом­ного магнитика можно изменить двумя путями:

а — горизонтальным магнитным полем, направленным всегда под прямым уг­лом к m ; б— осциллирующим полем.

Такое поле работает очень хорошо, однако нисколько не хуже действует и переменное горизонтальное поле. Если у нас есть горизонтальное поле В', которое всегда направлено по оси х (в положительную или отрицательную сторону) и которое ос­циллирует с частотой w p, тогда через каждые полпериода дей­ствующая на магнитный момент пара сил переворачивается, так что получается суммарный эффект, который почти столь же эффективен, как и вращающееся магнитное поле. С точки зрения классической физики мы бы ожидали при этом измене­ния компоненты магнитного момента вдоль оси z, если у нас есть очень слабое магнитное поле, осциллирующее с частотой, в точности равной w p. Разумеется, по классической физике m г должно изменяться непрерывно, но в квантовой механике z-компонента магнитного момента не может быть непрерывной. Она должна неожиданно «прыгать» от одного значения до дру­гого. Я сравнивал следствия классической и квантовой меха­ники, чтобы дать вам понятие о том, что может происходить классически, и как это связано с тем, что происходит на самом деле в квантовой механике. Обратите внимание, между прочим, что в обоих случаях ожидаемая резонансная частота одна и та же.

Еще одно дополнительное замечание. Из того, что мы гово­рили о квантовой механике, не видно, почему переходы не могут происходить при частоте 2w р . Оказывается, что в классическом случае этому совершенно нет никакого аналога, но в квантовой механике такие переходы невозможны, по крайней мере в описанном нами способе вынужденных переходов. При гори­зонтальном осциллирующем магнитном поле вероятность того, что частота 2w pвызовет скачок сразу на два шага, равна нулю. Все переходы, будь то переход вверх или вниз, предпочитают происходить только при частоте w р .

Вот теперь мы готовы к описанию метода Раби. Здесь мы опишем только, как этот метод измерения магнитных моментов работает в случае частиц со спином 1/ 2. Схема аппаратуры пока­зана на фиг. 35.5.

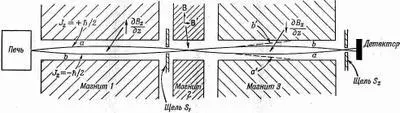
Фиг. 35.5. Схема установки Раби в опытах с молекулярными пучками.