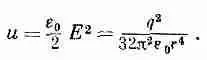
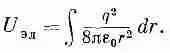
Чтобы получить полную энергию, нужно эту плотность проинтегрировать по всему пространству. Используя элемент объема 4pr 2/dr, найдем полную энергию, которую мы обозначим через U эл :
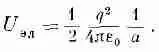
Это выражение интегрируется очень просто. Нижний предел интегрирования равен а, а верхний — бесконечности, поэтому
(28.1)
Если вместо q подставить заряд электрона q e и обозначить символом e 2 комбинацию q e 2/4pe 0, то получим
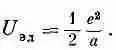
(28.2)
Все идет хорошо до тех пор, пока мы не переходим к точечному заряду, т. е. пока мы не положим а = 0. Но как только мы переходим к точечному заряду, начинаются все наши беды. И все потому, что энергия поля изменяется обратно пропорционально четвертой степени расстояния, интеграл по объему становится расходящимся, а количество энергии, окружающей точечный заряд, оказывается бесконечным.
Но чем, собственно, плоха бесконечная энергия? Есть ли какая-то реальная трудность в том, что энергия никуда не может уйти от заряда и обречена навсегда оставаться около него? Досадно, конечно, что величина оказалась бесконечной, но главный вопрос в том — есть ли здесь какой-нибудь наблюдаемый физический эффект? Чтобы ответить на него, нужно обратиться не к энергии, а к чему-то другому. Нас может, скажем, заинтересовать, как изменяется энергия, когда заряд движется. Если при этом окажется бесконечным изменение, то дело совсем плохо.
§ 2. Импульс поля движущегося заряда
Возьмем равномерно движущийся электрон и предположим на минуту, что скорость его мала по сравнению со скоростью света. С таким движущимся электроном всегда связан какой-то импульс — даже если у электрона до того, как он был заряжен, не было никакой массы — это импульс электромагнитного поля. Мы покажем, что для малых скоростей он пропорционален скорости v и совпадает с ней по направлению. В точке Р, находящейся на расстоянии r от центра заряда и под углом 6 к линии его движения (фиг. 28.1), электрическое поле радиально, а магнитное, как мы видели, равно vXE/c 2. Плотность же импульса, в соответствии с формулой (27.21), будет
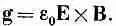
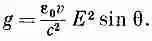
Она обязательно направлена по линии движения, как это видно из рисунка, и по величине равна
Поле симметрично относительно линии движения заряда, поэтому поперечные компоненты дадут в сумме нуль, и полученный в результате импульс будет параллелен скорости v.
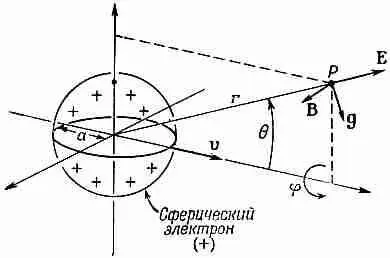
Фиг. 28.1. Поля Е и В и плотность импульса g для положительного электрона.
Для отрицательного электрона поля Е и В повернуты в обратную сторону, но g остается тем же.
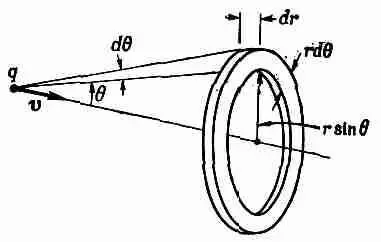
Фиг. 28.2. Элемент объема 2pr 2 sinqdqdr, используемый при вычислении импульса поля.
Величину составляющей вектора g в этом направлении, равную g sinq, нужно проинтегрировать по всему пространству. В качестве элемента объема возьмем кольцо, плоскость которого перпендикулярна v (фиг. 23.2). Объем его равен 2pr 2sinqdqdr . Полный импульс будет при этом
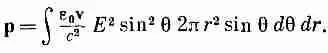
Поскольку Е не зависит от угла q (для v< то по углу можно немедленно проинтегрировать:
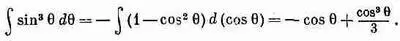
Интегрирование по q ведется в пределах от 0 до p, так что этот интеграл дает просто множитель 4/ 3, т. е.
Читать дальше

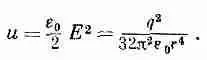
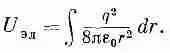
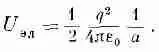
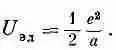
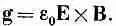
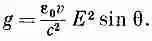


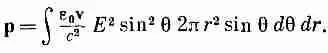
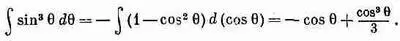



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
