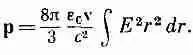
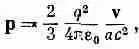
А такой интеграл (для v<<���с) мы только что вычисляли, чтобы найти энергию; он равен q 2 /16p 2 e 0 2 a, так что
или
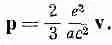
(28.3)
Импульс поля, т. е. электромагнитный импульс, оказался пропорциональным v. В частности, тоже самое выражение получилось бы для частицы с массой, равной коэффициенту пропорциональности при v. Вот почему этот коэффициент пропорциональности мы можем назвать электромагнитной массой m эм , т. е. положить
§ 3. Электромагнитная масса
Откуда же вообще возникло понятие массы? В наших законах механики мы предполагали, что любому предмету присуще некое свойство, называемое массой. Оно означает пропорциональность импульса предмета его скорости. Теперь же мы обнаружили, что это свойство вполне понятно — заряженная частица несет импульс, который пропорционален ее скорости. Дело можно представить так, как будто масса — это просто электродинамический эффект. Ведь до сих пор причина возникновения массы оставалась нераскрытой. И вот, наконец, в электродинамике нам представилась прекрасная возможность понять то, чего мы никогда не понимали раньше. Прямо как с неба (а точнее, от Максвелла и Пойнтинга) свалилось на нас объяснение пропорциональности импульса любой заряженной частицы ее скорости через электромагнитные свойства.
Но давайте все-таки встанем на более консервативную точку зрения и будем говорить, по крайней мере временно, что имеется два сорта масс и что полный импульс предмета должен быть суммой механического и электромагнитного импульсов. Причем механический импульс равен произведению «механической» массы m мехна скорость v. В тех экспериментах, где масса частицы измеряется, например, определением импульса или «кручением на веревочке», мы находим ее полную массу. Импульс равен произведению именно полной массы (m мех +m эм ) на скорость. Таким образом, наблюдаемая масса может состоять из двух (а может быть, и из большего числа, если мы учтем другие поля) частей: механической и электромагнитной. Мы знаем, что наверняка имеется электромагнитная часть; для нее у нас есть даже формула. А сейчас появилась увлекательная возможность выбросить механическую массу совсем и считать массу полностью электромагнитной.
Посмотрим, каков должен быть размер электрона, если «механическая» часть массы полностью отсутствует. Это можно выяснить, приравнивая электромагнитную массу (28.4) наблюдаемой массе электрона, т. е. m е . Получаем
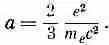
(28.5)
Величина
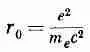
(28.6)
называется «классическим радиусом электрона» и равна она 2,82X10 =13 см,
т. е. одной стотысячной диаметра атома.
Почему радиусом электрона названа величина r 0, а не а? Потому что мы можем провести те же самые расчеты с другим распределением заряда. Мы можем взять его равномерно размазанным по всему объему шара или наподобие пушистого шарика. Например, для заряда, равномерно распределенного по всему объему сферы, коэффициент 2/ 3заменяется коэффициентом 4/ 5. Вместо того чтобы спорить, какое распределение правильно, а какое нет, было решено взять в качестве «номинального» радиуса величину r 0. А разные теории приписывают к ней свой коэффициент.
Давайте продолжим наше обсуждение электромагнитной теории массы. Мы провели расчет для v<<���с, а что произойдет при переходе к большим скоростям? Первые попытки вычисления привели к какой-то путанице, но позднее Лоренц понял, что при больших скоростях заряженная сфера должна сжиматься в эллипсоид, а поля должны изменяться согласно полученным нами для релятивистского случая в гл. 26 формулам (26.6) и (26.7). Если вы проделаете все вычисления для р в этом случае, то получите, что для произвольной скорости v импульс умножается еще на 1/Ц(1- v 2 /c 2 ) , т. е.
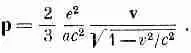
Читать дальше

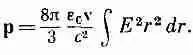
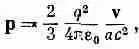
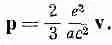
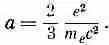
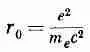
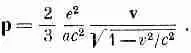



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
