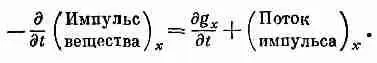
Теперь мне бы хотелось поговорить об импульсе поля. Поле обладает энергией; точно так же в единице объема оно обладает каким-то импульсом. Обозначим плотность импульса через g. Импульс, разумеется, может иметь различные направления, поэтому g должно быть вектором. Временно мы будем говорить об одной компоненте и для начала возьмем x-компоненту. Поскольку любая компонента импульса сохраняется, то мы можем сразу написать закон примерно такого вида:
Левая часть тривиальна. Скорость изменения импульса вещества равна просто действующей на него силе. Для частиц F=q(E+vXB), а для распределенных зарядов на единицу объема действует сила F=(rE+jXB). Однако слагаемое «поток импульса» несколько странно. Оно не может быть дивергенцией какого-то вектора, ибо это не скаляр, а скорее x-компонента некоторого вектора. Но как бы то ни было оно должно иметь вид
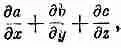
поскольку x-компонента импульса должна течь в каком-либо из трех направлений. Во всяком случае, каковы бы ни были а, b и с, такая комбинация предполагается равной потоку x-компоненты импульса.
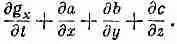
Дальше по правилам той же самой игры напишем rЕ+jXB только через Е и В, исключив плотность заряда r и плотность тока j и затем жонглируя слагаемыми и произведя подстановку, получаем
Сопоставляя затем разные слагаемые, мы должны найти выражения для g x , a, b и с. В общем, здесь масса работы, но мы не собираемся заниматься ею. Вместо этого мы найдем только выражение для плотности импульса g и притом совсем другим способом.
В механике есть очень важная теорема, которая говорит: каков бы ни был поток энергии любого вида (энергия поля или какой-то другой сорт энергии), произведение ее количества, прошедшего через единицу площади в единицу времени, на 1/с 2равно импульсу в единице объема пространства. В случае электродинамики эта теорема говорит, что g равно вектору Пойнтинга, поделенному на с 2:
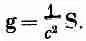
(27.21)
Так что вектор Пойнтинга дает нам не только поток энергии, но после деления на с 2и плотность импульса. Этот же результат получился бы из анализа, который мы только что предполагали проделать, однако более заманчиво воспользоваться общей теоремой. Сейчас мы рассмотрим несколько интересных примеров и рассуждений, призванных убедить вас в справедливости этой общей теоремы.
Первый пример: возьмем множество заключенных в ящик частиц. Пусть, скажем, их будет N штук на кубический метр, и пусть они движутся вдоль ящика со скоростью v. Рассмотрим теперь воображаемую плоскость, перпендикулярную к v. Поток энергии через единицу площади этой плоскости в секунду равен Nv (т. е. числу частиц, пересекающих плоскость за секунду), умноженному на энергию каждой частицы. Энергия же каждой частицы будет m 0c 2/Ц(l-v 2/c 2). Так что поток энергии равен
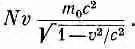
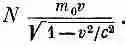
Но импульс каждой частицы равен m 0 v Ц( 1-v 2 /c 2 ), откуда плотность импульса будет
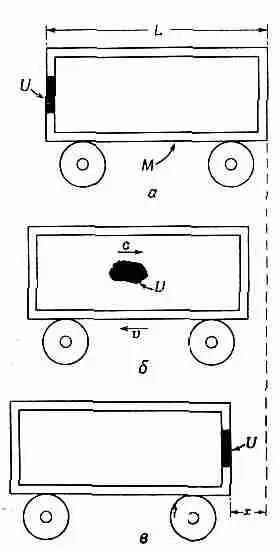
Фиг. 27.7. Порция энергии U, двигаясь со скоростью с, несет импульс, равный U/c.
что в полном согласии с теоремой как раз равно 1/с 2на поток энергии. Таким образом, для пучка частиц теорема оказывается верной.
Верна она и для света. При изучении света (см. вып. 3) мы установили, что, когда происходит поглощение света, поглотителю передается некоторое количество импульса. Действительно, в гл. 34 (вып. 3) мы видели, что импульс равен поглощенной энергии, деленной на с [уравнение (34.24)]. Пусть U 0 будет энергией, падающей в секунду на единичную площадь, тогда переданный той же поверхности за то же время импульс равен U 0 /c. Но импульс распространяется со скоростью с, так что его плотность перед поглотителем должна быть равна U 0/с 2. Теорема снова справедлива.
Читать дальше

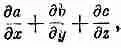
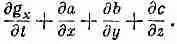
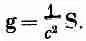
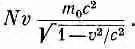
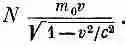




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
