Ричард Фейнман - 2. Пространство. Время. Движение

При применении теоремы о параллельных осях важно пом­нить, что ось I ц должна быть параллельна оси, относительно которой мы хотим вычислять момент инерции.

Стоит, пожалуй, упомянуть еще об одном свойстве, которое часто бывает очень полезно при нахождении момента инерции некоторых типов тел. Оно состоит в следующем: если у нас есть плоская фигура и тройка координатных осей с началом коор­динат, расположенным в этой плоскости, и осью r, направлен­ной перпендикулярно к ней, то момент инерции этой фигуры относительно оси z равен сумме моментов инерции относительно осей х и у. Доказывается это совсем просто. Заметим, что

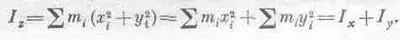
(поскольку все z i=0). Аналогично,

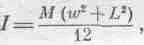
Момент инерции однородной прямоугольной пластинки, на­пример с массой М, шириной w и длиной L относительно оси, перпендикулярной к ней и проходящей через ее центр, равен просто

поскольку момент инерции относительно оси, лежащей в плос­кости пластинки и параллельной ее длине, равен Mw 2/12, т. е. точно такой же, как и для стержня длиной w, а момент инерции относительно другой оси в той же плоскости равен ML 2/12, такой же, как и для стержня длиной L.

Итак, перечислим свойства момента инерции относительно данной оси, которую мы назовем осью z:

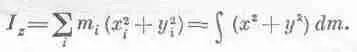
1. Момент инерции равен

2. Если предмет состоит из нескольких частей, причем момент инерции каждой из них известен, то полный момент инерции равен сумме моментов инерции этих частей.

3. Момент инерции относительно любой данной оси равен моменту инерции относительно параллельной оси, про­ходящей через центр масс, плюс произведение полной массы на квадрат расстояния данной оси от центра масс.

4. Момент инерции плоской фигуры относительно оси, пер­пендикулярной к ее плоскости, равен сумме моментов инерции относительно любых двух других взаимно пер­пендикулярных осей, лежащих в плоскости фигуры и пе­ресекающихся с перпендикулярной осью.

Таблица 19,1 · простые примеры моментов инерции

В табл. 19.1 приведены моменты инерции некоторых элементарных фигур, имеющих однородную плотность масс, а

табл. 19.2 — моменты инерции некоторых фигур, которые могут быть получены из табл. 19.1 с использованием пере

численных выше свойств.

Таблица 19.2 · моменты инерции, полученные из табл. 19.1

§ 4. Кинетическая энергия вращения

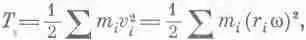
Продолжим изучение динамики вращения. При обсуждении аналогии между линейным и угловым движением в гл. 18 мы использовали теорему о работе, но ничего не говорили о кинети­ческой энергии. Какова будет кинетическая энергия твердого тела, вращающегося вокруг некоторой оси с угловой скоростью w? Используя нашу аналогию, можно немедленно угадать правильный ответ. Момент инерции соответствует массе, угло­вая скорость соответствует обычной скорости, так что кине­тическая энергия должна быть равна 1/ 2Iw 2. Так оно и есть на самом деле, и сейчас мы покажем это. Предположим, что тело вращается вокруг некоторой оси, так что каждая точка движет­ся со скоростью wr,-, где r i — расстояние от данной точки до оси. Если масса этой точки равна m i , то полная кинетическая энергия всего тела равна просто сумме кинетических энергий всех частиц

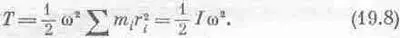
а поскольку w — постоянная, одна и та же для всех точек, то

В конце гл. 18 мы отмечали, что существуют очень интерес­ные явления, связанные с вращением не абсолютно твердого тела, способного изменять свой момент инерции. Именно, в примере с вращающимся столом у нас был момент инерции I 1и угловая скорость w 1при вытянутых руках. Согнув руки, мы изменили момент инерции до I 2, а угловую скорость — до w 2. Так как у нас нет никаких моментов сил относительно оси вра­щения стола, то момент количества движения должен остаться постоянным. Это означает, что I 1w 1=I 2w 2. А что можно ска­зать об энергии? Это очень интересный вопрос. Согнув руки, мы начинаем вращаться быстрее, но момент инерции при этом умень­шается и может показаться, что кинетическая энергия должна остаться той же самой. Это, однако, неверно, потому что в дей­ствительности сохраняется Iw, а не Iw 2. Сравним теперь кине­тические энергии в начале и в конце. В начале кинетическая энергия равна 1/ 2/Iw 2 1= 1/2Lw 1, где L=I 1w 1=I 2w 2— момент количества движения. Точно таким же образом кинетическая энергия в конце равна Т= 1/ 2Lw 2,а поскольку w 2>w 1, то кинетическая энергия в конце оказывается большей, чем в на­чале. Итак, вначале, когда руки были вытянуты, мы вращались с какой-то кинетической энергией, затем, согнув руки, мы стали вращаться быстрее и наша кинетическая энергия возросла. А как быть с законом сохранения энергии? Ведь должен же кто-то произвести работу, чтобы увеличить энергию? Это сделали мы сами! Но когда, в какой момент? Когда мы держим гантели гори­зонтально, то никакой работы не производим. Выпрямляя руки в стороны и сгибая их, мы тоже не можем произвести никакой работы. Это, однако, верно только, пока нет никакого вращения! При вращении же на гантели действует центробежная сила. Они стремятся вырваться из наших рук, так что, сгибая во время вращения руки, мы преодолеваем противодействие центробеж­ной силы. Работа, которая на это затрачивается, и составляет разницу в кинетических энергиях вращения. Вот откуда бе­рется этот добавок.