Пусть Джо для своих координатных осей х, у, z определял все моменты сил и все угловые моменты во всех плоскостях. Однако Мик направил свои оси х', у', z' по-другому. Чтобы немного облегчить задачу, предположим, что повернуты только оси x и y. Мик выбрал другие оси х' и у', а его ось z осталась той же самой. Это означает, что плоскости yz и zx у него новые, а поэтому моменты сил и угловые моменты у него тоже окажутся новыми. Например, его момент сил в плоскости х'у' окажется равным

x'F y '-y'F x ' и т. д. Следующая задача — найти связь между новыми и старыми моментами сил. Ее вполне можно решить, установив связь одного набора осей с другим. «Да это же напоминает то, что мы делали с векторами»,— скажете вы. Действительно, я собираюсь делать в точности то же самое. «А не вектор ли он, этот момент сил?» — спросите вы. Действительно, он — вектор, однако этого нельзя сказать просто так, без всякого математического анализа. Так что следующим этапом должен быть анализ. Однако мы не будем подробно обсуждать каждый шаг, а только покажем, как это все работает. Моменты сил, вычисленные Джо, равны

В этом месте мы сделаем отступление и заметим, что в подобных случаях, если оси координат выбраны неправильно, для некоторых величин получается неверный знак. Почему бы не написать t yz =zF y -yF z ? Этот вопрос связан с тем обстоятельством, что система координат может быть либо «левая», либо «правая». Однако выбрав (произвольно) знак, скажем, у t xy , можно всегда определить правильное выражение для остальных двух величин путем замены по какой-либо из двух схем:

Теперь Мик подсчитывает моменты сил в своей системе.
Пусть одна система координат повернута на угол q по отношению к другой, так что ось z осталась той же самой. (Угол q ничего не имеет общего с вращением объекта или с чем-то происходящим внутри системы координат. Это просто связь между осями, используемыми одним человеком, и осями, используемыми другим. Мы предполагаем, что он остается постоянным.) При этом координаты в двух системах связаны так:
x'=x cosq+ysinq,
y'=у cosq- х sinq, (20.3)
z'=z.
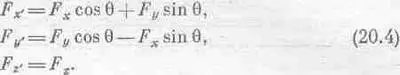
Точно таким же образом, поскольку сила является вектором, она преобразуется в новой системе координат так же, как х, у и z. Просто, по определению, объект называется вектором тогда и только тогда, когда различные его компоненты преобразуются как х, у и z
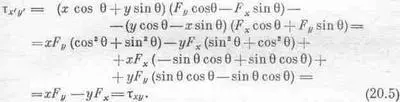
Теперь можно определить, как преобразуется момент силы. Для этого в уравнение (20.2) нужно просто подставить вместо х', у' и z' выражение (20.3), а для F x ' , F y ' , и F z ' -— выражение (20.4). В результате для t x ' y 'получается длинный ряд членов, но оказывается (и на первый взгляд это удивительно), что все сводится просто к выражению xF y -yF x , которое, как известно, является моментом силы в плоскости ху:
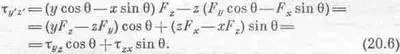
Результат совершенно ясен: ведь мы только повернули оси, лежащие в плоскости ху, при этом момент относительно оси z в этой плоскости не отличается от прежнего: ведь плоскость-то осталась той же самой! Более интересно выражение для t V ' Z ' . Здесь уже мы имеем дело с новой плоскостью. Если теперь повторить то же самое с плоскостью y'z', то получим
И наконец, для плоскости z'x'
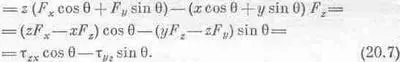

Мы хотели найти правило для определения момента сил в новой системе через момент сил в старой и нашли его. Как можно запомнить это правило? Если внимательно посмотреть на уравнения (20.5)—(20.7), то нетрудно увидеть, что между ними и уравнениями для х, у и z существует тесная связь. Если каким-то образом мы бы могли назвать t ху z-компонентой чего-то, скажем z-компонентой вектора t, то все было бы в порядке: уравнение (20.5) мы бы понимали как преобразование вектора t, ибо z-компонента его, как это и должно быть, оставалась бы неизменной. Аналогично, если связать плоскость yz с x -ком понентой новоиспеченного вектора, а плоскость zx с у-компо нентой, то закон преобразования будет выглядеть так:
Читать дальше




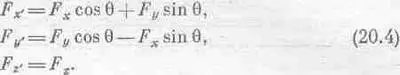
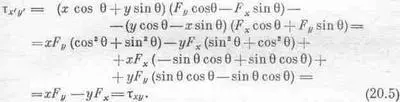
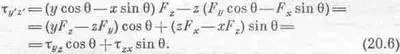
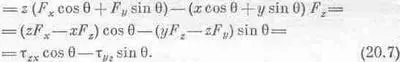




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)

