Например, если нам нужно найти центр масс прямоугольного треугольника с основанием D и высотой H (фиг. 19.2), то это делается следующим образом.
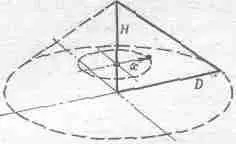
Фиг. 19.2. Прямоугольный треугольник и прямой круговой конус, образованный вращением этого треугольника.
Вообразите себе ось, проходящую вдоль H, и поверните треугольник на 360° вокруг этой оси. Это дает нам конус. Расстояние, которое проходит x-координата центра масс, равно 2 p х, а площадь области, которая двигалась, т. е. площадь треугольника, равна 1 / 2 HD. Произведение расстояния, пройденного центром масс, на площадь треугольника равно объему конуса, т. е. 1 / 3 p D 2 H. Таким образом, (2 p х)( 1 / 2 HD)= 1 / 3 p D 2 H, или x=D/3. Совершенно аналогично вращением вокруг второго катета или просто по соображениям симметрии находим, что у=Н/3. Вообще центр масс любого однородного треугольника находится в точке пересечения трех его медиан (линий, соединяющих вершину треугольника с серединой противоположной стороны), которая отстоит от основания на расстоянии, равном 1/ 3длины каждой медианы.
Как это увидеть? Рассеките треугольник линиями, параллельными основанию, на множество полосок. Заметьте теперь, что медиана делит каждую полоску пополам, следовательно, центр масс должен лежать на медиане.
Возьмем теперь более сложную фигуру. Предположим, что требуется найти положение центра масс однородного полукруга, т. е. круга, разрезанного пополам. Где будет находиться центр масс в этом случае? Для полного круга центр масс расположен в геометрическом центре, но для полукруга найти его положение труднее. Пусть r — радиус круга, а x — расстояние центра масс от прямолинейной границы полукруга. Вращая его вокруг этого края как вокруг оси, мы получаем шар. При этом центр масс проходит расстояние 2 p х, а площадь полукруга равна 1/ 2pr 2(половине площади круга). Так как объем шара равен, конечно, 4pr 3/3, то отсюда находим
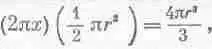
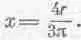
или
Существует еще другая теорема Паппа, которая фактически является частным случаем сформулированной выше теоремы, а потому тоже справедлива. Предположим, что вместо твердого полукруга мы взяли полуокружность, например кусок проволоки в виде полуокружности с однородной плотностью, и хотим найти ее центр масс. Оказывается, что площадь, которая «заметается» плоской кривой при ее движении, аналогичном вышеописанному, равна расстоянию, пройденному центром масс, умноженному на длину этой кривой. (Кривую можно рассматривать как очень узкую полоску и применять к ней предыдущую теорему.)
§ 3. Вычисление момента инерции
Рассмотрим теперь проблему определения момента инерции различных тел. Общая формула для нахождения момента инерции объекта относительно оси z имеет вид
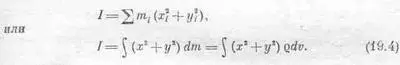
Иными словами, нужно сложить все массы, умножив каждую из них на квадрат ее расстояния до оси (z 2 i+y 2 i). Заметьте, что это верно даже для трехмерного тела, несмотря на то, что расстояние имеет такой «двумерный вид». Впрочем, в большинстве случаев мы будем ограничиваться двумерными телами.
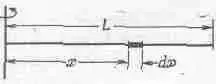
В качестве простого примера рассмотрим стержень, вращающийся относительно оси, проходящей через его конец и перпендикулярной к нему (фиг. 19.3).
Фиг. 19.3. Прямой стержень, вращающийся вокруг оси, проходящей через один из его концов.
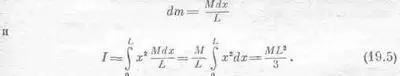
Нам нужно просуммировать теперь все массы, умноженные на квадраты расстояния х (в этом случав все у — нулевые). Под суммой, разумеется, я имею в виду интеграл от x 2 , умноженный на «элементики» массы. Если мы разделим стержень на кусочки длиной dx, то соответствующий элемент массы будет пропорционален dx, а если бы dx составляло длину всего стержня, то его масса была бы равна М. Поэтому
Читать дальше


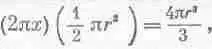
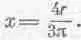
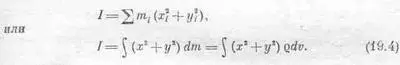

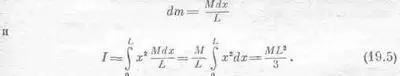



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)

