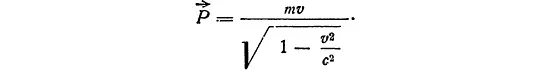Если ускорения В «велики», то, используя только специальную теорию, вообще ничего определенного нельзя сказать. Но если прибегнуть к общей теории относительности, можно показать, что В должны отставать от А .
И наконец, если ускорялись и В и A , весь вопрос следует адресовать к общей теории, так как в этом случае могут осуществляться самые разные варианты.
Так что ответ на кажущийся парадокс скрыт в неравноправии двух часов: А и B . Если они разъехались, а затем встретились, то хотя бы одни часы испытали действие ускорений [80] .
все недостатки которой должно искупить содержание

Эйнштейн. Законы механики
(масса и энергия)
Законы механики Эйнштейна поражают своей необычностью человека, воспитанного на классических представлениях, хотя между релятивистской механикой и механикой Ньютона значительно больше общего, чем может показаться на первый взгляд.
Начнем с того, что первый закон Ньютона остается неизменным и в релятивистской механике — в инерциальной системе отсчета тело, свободное от действия внешних сил, сохраняет неизменным свой импульс.
И опять рассуждения.
Третий закон механики Ньютона — равенство действия и противодействия — также остается в механике теории относительности. Снова можно утверждать, что «если два тела взаимодействуют между собой, то их суммарный импульс остается неизменным».
Собственно говоря, остается неизменным и второй закон механики. По-прежнему сила равна скорости изменения импульса:
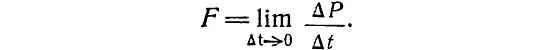
Второй закон Ньютона в релятивистской механике.
Но если содержание второго закона прежнее, конкретная его форма существенно меняется. Нам придется принять на веру, что в релятивистской механике импульс тела определяется выражением:
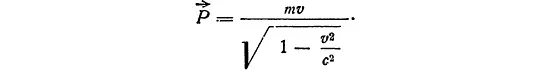
Выводить эту формулу мы не в состоянии и потому отметим только, что определение импульса выглядит довольно естественно и правдоподобно.
Во-первых, при скоростях, много меньших скорости света, мы получаем (как и должно быть) знакомое классическое выражение для импульса P = mv .
С другой стороны, по мере приближения скорости тела к скорости света импульс стремится к бесконечности, что тоже понятно, так как полностью соответствует тому обстоятельству, что никакое материальное тело нельзя разогнать до скорости, равной скорости света.
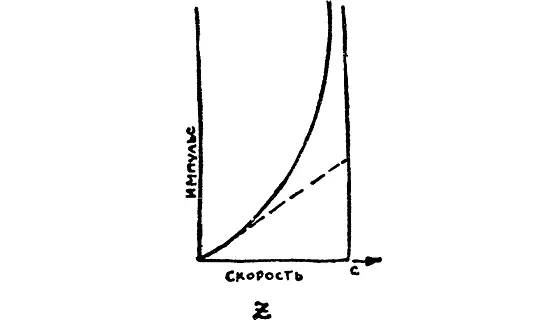
На графике очень хорошо видно, как связан истинный импульс тела с приближенным классическим выражением.
Сплошная линия — это релятивистское выражение для импульса, а пунктирная — классическое. Даже при очень больших, с «житейской точки зрения», скоростях релятивистская формула почти совпадает с классической.
При скорости в 30 километров в секунду [81] , используя классическое выражение, мы занижаем импульс на одну вторую миллионной доли процента.
Поэтому ясно, что даже при расчете движения космических ракет никому не приходит в голову учитывать релятивистские эффекты. Очевидно, еще более нелепо использовать строгие формулы теории относительности при рассмотрении тех значительно более медленных движений, с которыми мы имеем дело в повседневной технике. В этих случаях великолепно оправдывается первое приближение — механика Ньютона.
Но в нашем веке инженерам пришлось встретиться с большим числом чисто технических задач, для решения которых необходима механика Эйнштейна. Элементарные частицы — электроны, протоны — разгоняются в современных ускорителях до скоростей, предельно близких к скорости света.
Если электрон ускорять при помощи сравнительно скромной разности потенциалов в 1 миллион вольт, он приобретет скорость 0,92 с . При такой скорости импульс, вычисленный по классической формуле, уже в 3 раза ниже истинного значения. Излишне пояснять, что при расчетах ускорителей элементарных частиц используют строгие формулы релятивистской механики. Так что в наше время теория Эйнштейна используется и в инженерной физике. Вероятно, так же излишне упоминать, что практика прекрасно согласуется с формулами Эйнштейна.
Читать дальше


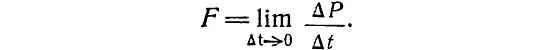 Второй закон Ньютона в релятивистской механике.
Второй закон Ньютона в релятивистской механике.