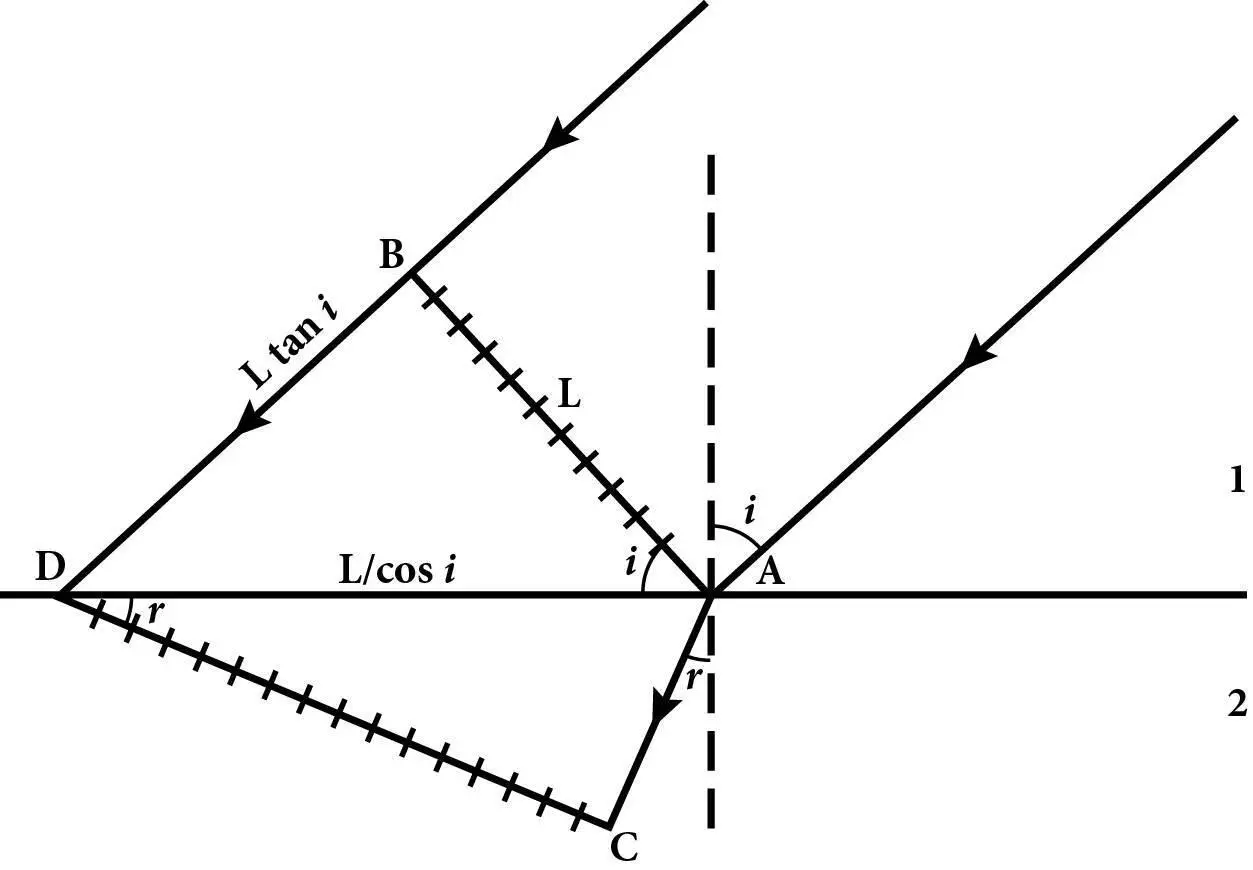
φ = 4 r – 2 i .
Ми можемо виразити r , залежну від i :
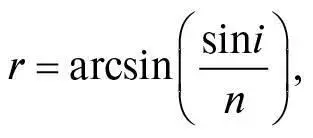
де для будь-якого x значення arcsin x дорівнює куту (зазвичай взятому між −90° і +90°), синус якого дорівнює x . Розрахунки для n = 4/3, подані в розділі 13, демонструють, що φ зростає від нуля за i = 0 до максимального значення приблизно в 42°, а потім падає приблизно до 14° за i = 90°. Графік φ залежно від i горизонтальний у його максимумі, тому світло має тенденцію виходити з краплини під кутом заломлення φ, близьким до 42°.
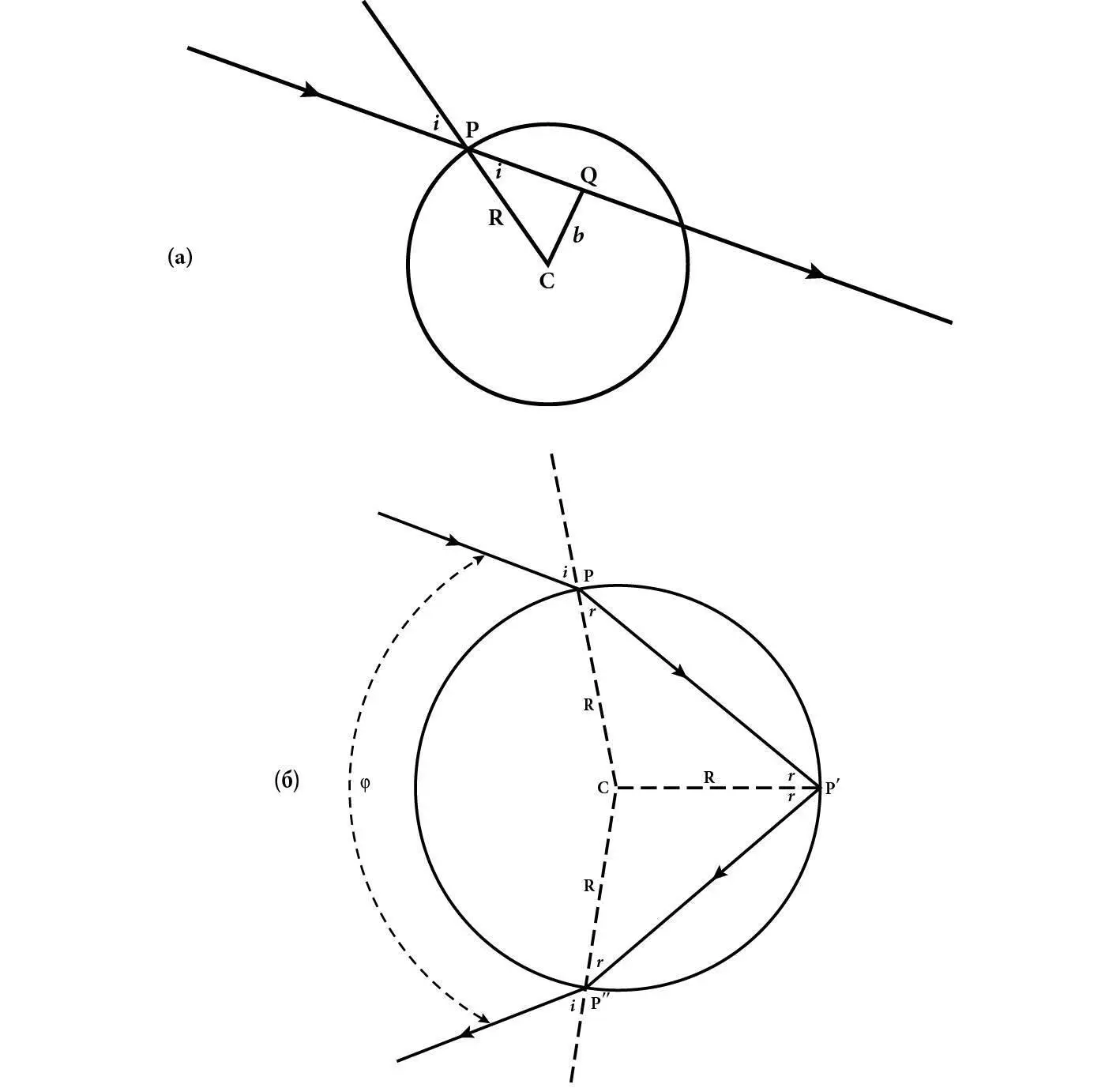
Рис. 22.Шлях променя сонячного світла у сферичній краплі води. Промінь зображений суцільними лініями зі стрілками: він входить до краплини в точці P, де утворює кут i з перпендикуляром до поверхні; a) шлях променя, якби заломлення не відбувалося, де Q – точка максимального наближення променя до центра краплини C; б) промінь заломлюється на вході до краплини в точці P, відбивається від задньої поверхні краплини в точці P´, а потім заломлюється знову на виході з краплини в Pʺ. Пунктирні лінії з’єднують центр краплини C з точками, де промінь зустрічається з поверхнею краплини.
Якщо поглянути в туманне небо, ставши до Сонця спиною, ми побачимо світло, відбите назад, під кутом між лінією нашої прямої видимості та променями, що йдуть від сонця, що дорівнює приблизно 42°. Ці напрямки утворюють дугу, яку зазвичай ми бачимо такою, що йде від земної поверхні вгору до неба, а потім знову вниз до поверхні. Оскільки n трохи залежить від кольору світла, кути заломлення φ для різних кольорів будуть різні, тому ця дуга розбивається на різні кольори. Це і є райдуга.
Нескладно вивести аналітичну формулу, що дає нам максимальне значення φ для будь-якого значення показника заломлення n . Щоб знайти максимум φ, зауважмо той факт, що цей максимум відповідає такому куту падіння i , за якого графік φ залежно від i горизонтальний, тож зміна δφ (дельта фі) кута φ, породжена мізерно малою зміною δ i кута i , зникає до першого порядку δ i . Щоб використати цю умову, ми застосуємо стандартну формулу диференціального числення, згідно з якою в разі зміни δ x аргументу x , зміна arcsin x дорівнює:
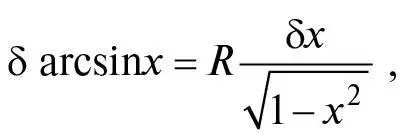
де R = 360°/2π, якщо arcsin x вимірюють у градусах. Отже, коли кут падіння змінюється на величину δ i , то кут заломлення змінюється на таку величину:
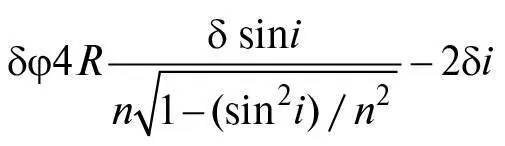
або, оскільки δ sin i = cos i δ i/R ,
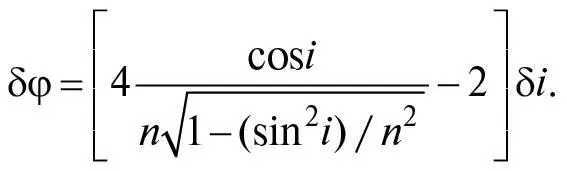
Отже, умова для максимуму φ така, що:
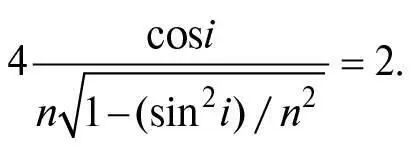
Піднісши обидві частини рівняння до квадрата та використовуючи формулу cos2 i = 1 − sin2 i (що випливає з теореми Піфагора), можемо знайти значення sin i :
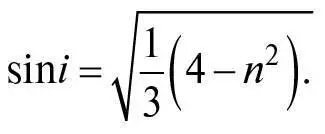
За такого значення кута падіння φ набуває свого максимального значення:
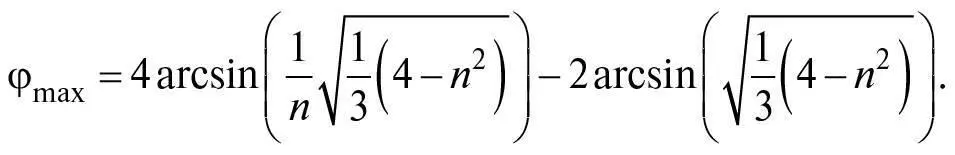
За n = 4/3 максимальне значення φ досягають за b / R = sini = 0,86, для якого i = 59,4°, r = 40,2°, а φmax = 42,0°.
30. Виведення закону заломлення світла із хвильової теорії світла
Закон заломлення світла, який, як описано в технічній примітці 28, можна вивести з припущення, що відбиті промені світла йдуть шляхом найменшого часу, можна також вивести на основі хвильової теорії світла. За словами Гюйґенса, світло є збуренням у середовищі, яким може бути якийсь прозорий матеріал або простір, що є очевидно порожнім. Фронтом цього збурення є лінія, що рухається вперед у напрямку, перпендикулярному цьому фронту, зі швидкістю, характерною для цього середовища.
Читать дальше

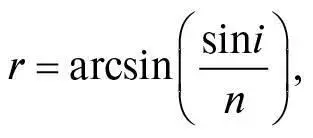

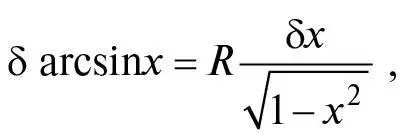
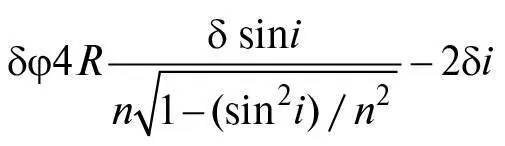
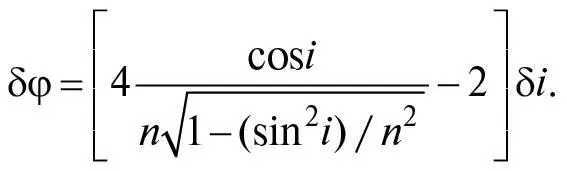
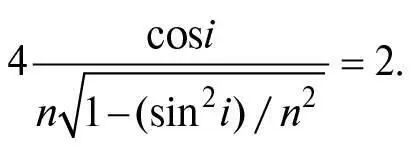
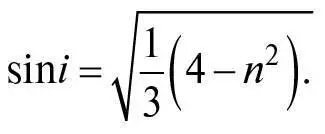
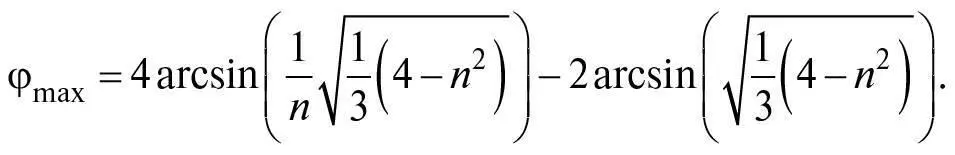






![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)




