Стивен Вайнберг - Пояснюючи світ

28. Виведення закону заломлення світла з принципу найменшого часу

Герон Александрійський вивів закону відбиття світла (кут відбиття дорівнює куту падіння), припустивши, що шлях променя світла від об’єкта до дзеркала, а потім до ока якомога коротший. Він міг би так само припустити, що якомога коротшим є час, за який промінь світла долає цей шлях, оскільки час проходження світлом будь-якої відстані дорівнює цій відстані, поділеній на швидкість світла, а під час відбиття швидкість світла не змінюється. З другого боку, заломлення променя світла відбувається, коли він проходить межу між середовищами (наприклад, між повітрям та склом), у яких швидкість світла різна, тож ми маємо розрізняти принципи найменшої відстані та найменшого часу. Лише з того факту, що промінь світла змінює напрям, коли переходить з одного середовища до іншого, ми знаємо, що заломлене світло не йде шляхом найменшої відстані, яким була б пряма. Радше, як показав Ферма, правильний закон заломлення світла можна вивести з припущення, що світло витрачає на шлях якнайменший час.

Щоб продовжити це виведення, припустімо, що промінь світла рухається від точки PА в середовищі А , у якому швидкість світла становить vA , до точки PB у середовищі B , у якому швидкість світла дорівнює vB . Щоб спростити опис, припустімо, що поверхня, яка розділяє ці два середовища, горизонтальна. Позначмо кути між променями світла в середовищах А і B та вертикальним напрямком i та r відповідно. Якщо точки PА та PB розташовані на вертикальних відстанях dА та dB від граничної поверхні, то горизонтальні відстані цих точок від точки, де промені перетинають цю поверхню, дорівнюють dА tg i та dB tg r відповідно, де символ tg позначає тангенс кута – відношення довжини протилежного катета до прилеглого у прямокутному трикутнику (див. рис. 21). Хоч ці відстані не зафіксовані наперед, їхня сума фіксована й дорівнює горизонтальній відстані L між точками PА та PB :

L = d А t tg i + d B t tg r .

Щоб обчислити час t , витрачений світлом на подолання шляху від PА до PB , зауважмо, що пройдені променем відстані в середовищах А і B дорівнюють dА /cos i та dB /cos r відповідно, де «cos» позначає косинус кута – відношення прилеглого катета до гіпотенузи у прямокутному трикутнику. Витрачений час дорівнює відстані, поділеній на швидкість, тому загальний витрачений час тут дорівнює:

Нам потрібно знайти загальне співвідношення між кутами i та r (що не залежить від L, dА та dB ), яке задовольняє такий кут i , за якого час t мінімальний, а r залежить від i так, щоб L залишалася фіксованою. Для цього розгляньмо δ i – нескінченно малу зміну δ (дельта) кута падіння i . Горизонтальна відстань між точками PА та PB фіксована, тому коли i змінюється на величину δ i , кут заломлення r має також змінюватися, скажімо, на величину δ r , за умови, що L незмінна. Крім того, у точці мінімуму графік t залежно від i повинен бути горизонтальний, бо якщо t збільшується або зменшується за якогось i , цей мінімум має відповідати якомусь іншому значенню i , де t менший. Це означає, що зміна t , спричинена мізерно малою зміною δ i , має зникнути, хоча б до першого порядку величини δ i . Тому, щоб знайти шлях, на подолання якого променю світла знадобиться найменше часу, ми можемо визнати умову, що в разі зміни обох кутів i та r зміни δ L та δ t мають зникнути хоча б до першого порядку δ i та δ r .

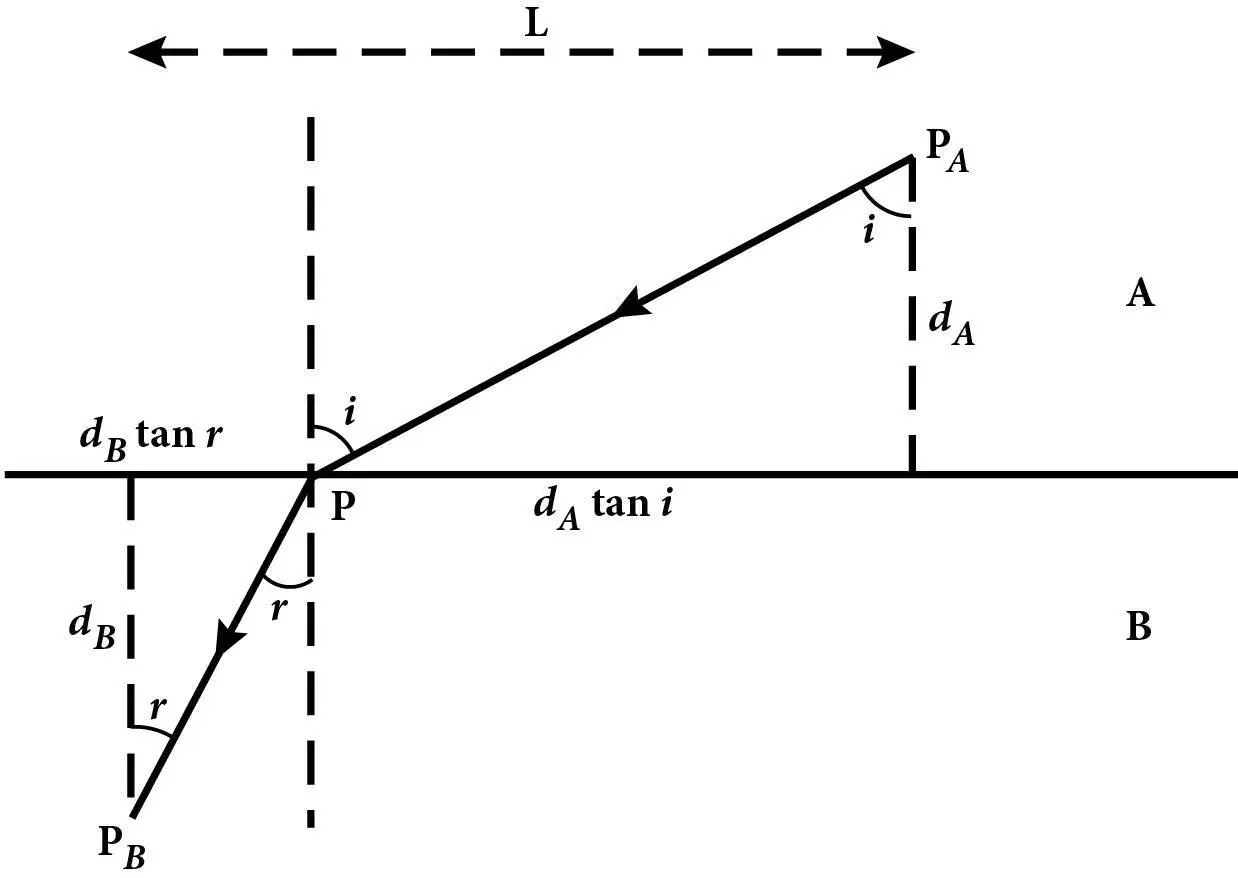
Рис. 21.Шлях заломлюваного променя світла. Горизонтальна лінія позначає поверхню, що розділяє два прозорі середовища А і B, у яких світло має різні швидкості vA та vB, а кути i та r вимірюють між променем світла та пунктирною вертикальною лінією, перпендикулярною до поверхні, що розділяє середовища. Суцільна лінія зі стрілками позначає шлях променя світла, що рухається від точки PА в середовищі А до точки P на межі середовищ, а потім до точки PB у середовищі B.

Щоб задовольнити цю умову, нам потрібні стандартні формули диференціального числення для зміни δtgθ (тета) та δ(1/cosθ), коли ми змінюємо кут θ на нескінченно малу величину δθ: