Параболи, як і еліпси, можна вважати конічними перерізами, але для парабол площина, що перерізає конус, паралельна поверхні конуса. Якщо припустити, що рівняння конуса, центральна вісь якого збігається з віссю z , має вигляд 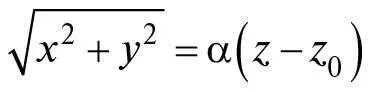 , а рівняння площини, паралельної конусу, просто y = α( z − z 0) з довільним z 0, то крива перетину конуса з площиною задовольняє умови рівності:
, а рівняння площини, паралельної конусу, просто y = α( z − z 0) з довільним z 0, то крива перетину конуса з площиною задовольняє умови рівності:
x 2 + α2( z 2 – 2 zz 0 + z 02) = α2( z 2 + 2 zz 0 + z 02).
Скоротивши члени α2 z 2 та α2 z 02, отримаємо таке рівняння:
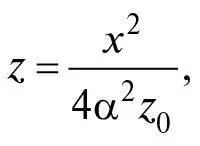
що є тим самим, що й наш попередній результат, у випадку, коли z0 = l/α2. Зверніть увагу, що параболу певної форми можна отримати перерізом будь-якого конуса з будь-яким значенням кутового параметра α (альфа), бо форма будь-якої параболи (на відміну від її положення та орієнтації) цілковито визначається параметром l, вимірюваним в одиницях довжини; нам не потрібно знати окремо жодного безрозмірного параметра на кшталт α чи ексцентриситету якогось еліпса.
27. Виведення закону заломлення за аналогією з тенісним м’ячиком
Декарт намагався вивести закон заломлення світла, з огляду на припущення, що промінь світла заломлюється, переходячи з одного середовища до іншого в такий самий спосіб, як тенісний м’ячик змінює траєкторію, коли пробиває тонку тканину. Припустімо, тенісний м’ячик зі швидкістю v A похило вдаряє в екран із тонкої тканини. Він дещо втратить швидкість, тож після пробивання екрана його швидкість буде v B < v A, але ми не очікуємо, що прохід м’ячика крізь тканину спричинить якусь зміну компоненти швидкості м’ячика, спрямованої вздовж тканини. Ми можемо накреслити прямокутний трикутник, катети якого будуть компонентами початкової швидкості м’ячика, що перпендикулярні та паралельні до тканини, а гіпотенуза дорівнюватиме v A. Якщо первинна траєкторія м’ячика утворює кут i з перпендикуляром до тканини, тоді компонента його швидкості, спрямована паралельно до тканини, дорівнює v Asin i (див. рис. 20). Так само, якщо після пробивання тканини траєкторія м’ячика утворює кут r із перпендикуляром до тканини, тоді компонента його швидкості, спрямована паралельно до тканини, дорівнює vB sin r . Використовуючи припущення Декарта, що проходження м’ячика крізь тканину може змінити лише компоненту швидкості, спрямовану перпендикулярно, а не паралельно до поверхні, отримуємо:
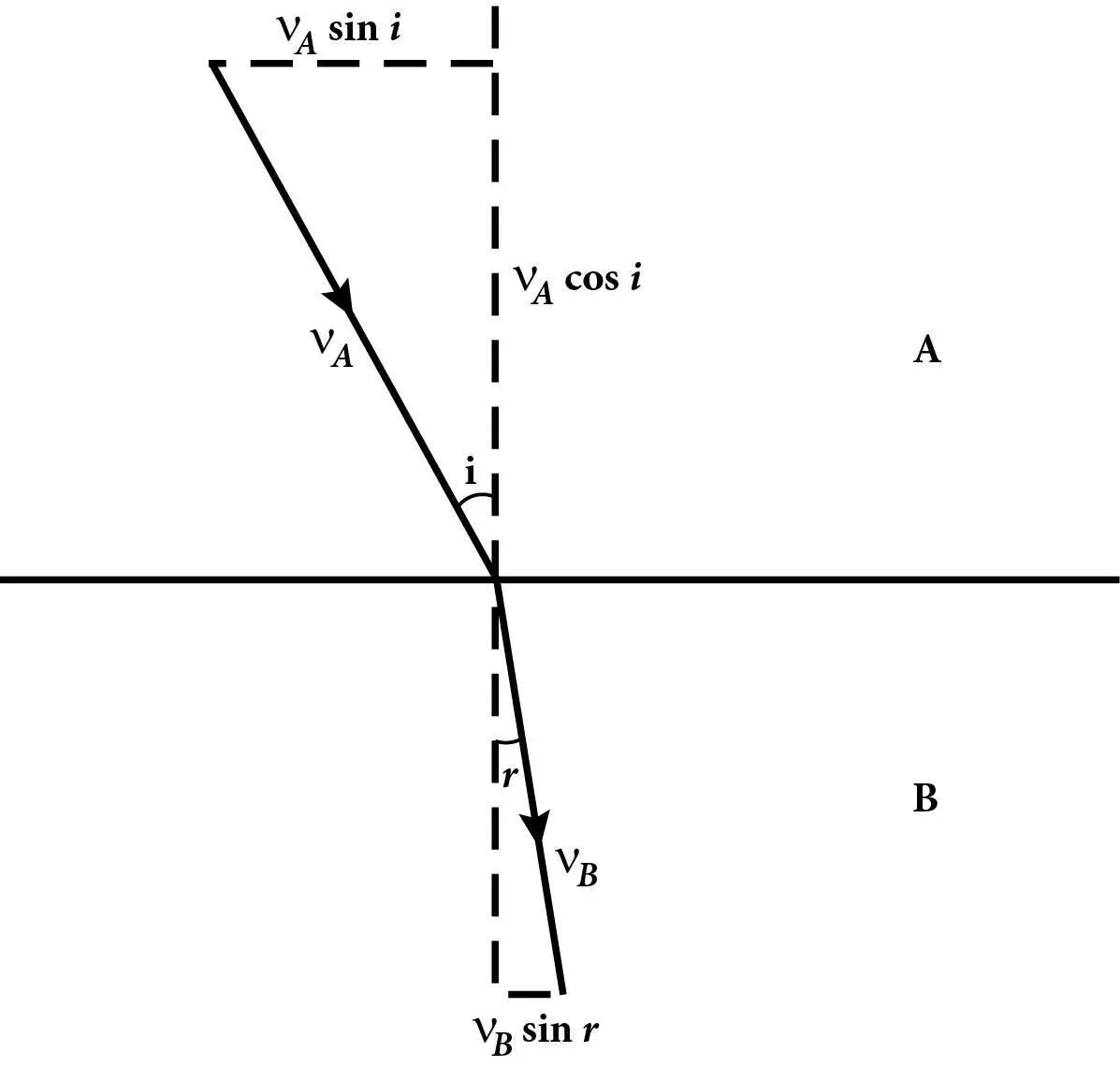
Рис. 20.Швидкості тенісного м’ячика. Горизонтальна лінія позначає екран із тканини, який пробиває тенісний м’ячик із початковою швидкістю vA та кінцевою швидкістю vB. Суцільні лінії зі стрілками вказують на величину та напрямки швидкості м’ячика до й після пробивання ним тканини. На цьому зображенні шлях м’ячика змінюється й відхиляється в бік перпендикуляра до тканини, як і у випадку, коли промені світла входять у середовище більшої густини. Це демонструє, що проходження м’ячика крізь тканину значно зменшує компоненту його швидкості, спрямовану вздовж тканини, усупереч припущенню Декарта.
vA sin i = vB sin r ,
а отже,
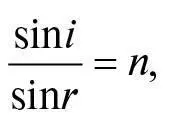 (1)
(1)
де n є величиною:
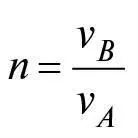 (2)
(2)
Рівняння (1) відоме як закон Снелліуса, який правильно описує заломлення світла. На жаль, аналогія між світлом і тенісним м’ячиком не працює, коли ми переходимо до рівняння (2), що визначає n . Оскільки для тенісних м’ячиків vB менша за vA , рівняння (2) дає нам n < 1, тоді як під час переходу світла з повітря до скла чи води n > 1. Крім того, немає жодних причин припускати, що для тенісних м’ячиків відношення vB / vA насправді не залежить від кутів i та r , а отже, рівняння (1) не корисне в його нинішньому вигляді.
Як показав Ферма, коли світло переходить із середовища, де його швидкість дорівнює vA , в інше середовище, де його швидкість дорівнює vB , показник заломлення n насправді дорівнює vA / vB , а не vB / vA . Декарт не знав, що світло рухається зі скінченною швидкістю, і запропонував непереконливе пояснення, чому n більше за одиницю, якщо А – це повітря, а B – вода. Для уявлень XVII століття, як-от теорія райдуги Декарта, це не мало значення, бо показник заломлення n вважали незалежним від кута падіння (що справедливо для світла, хоч і не для тенісних м’ячиків), а його значення брали зі спостережень заломлення, а не отримували з вимірювань швидкості світла в різноманітних середовищах.
Читать дальше

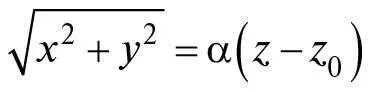 , а рівняння площини, паралельної конусу, просто y = α( z − z 0) з довільним z 0, то крива перетину конуса з площиною задовольняє умови рівності:
, а рівняння площини, паралельної конусу, просто y = α( z − z 0) з довільним z 0, то крива перетину конуса з площиною задовольняє умови рівності: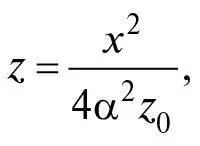

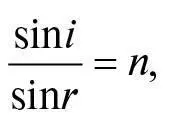 (1)
(1)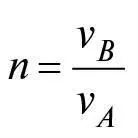 (2)
(2)




![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)




