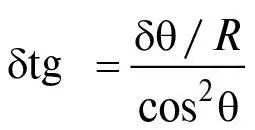
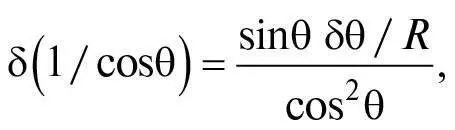
де R = 360°/2π = 57,293…°, якщо θ вимірюють у градусах (цей кут розміром в 1 радіан. Якщо θ вимірюють в радіанах, тоді R = 1). Використовуючи ці формули, ми знаходимо зміни L і t , коли змінюємо кути i та r на нескінченно малі величини δ i та δ r :
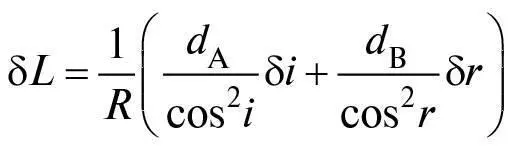
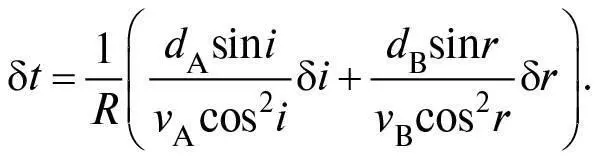
Визнана нами умова, що δ L = 0, говорить, що:
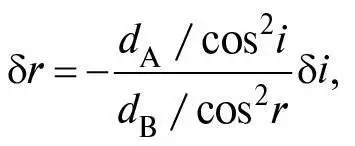
тому
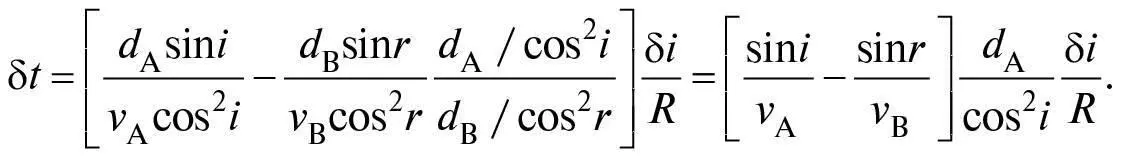
Щоб цей вираз дорівнював нулю, потрібно, щоб
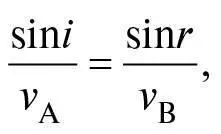
або, інакше кажучи,
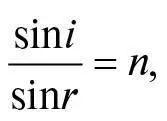
де показник заломлення n є співвідношенням швидкостей, заданим незалежно від кутів:
n = v А/ v B.
Це і є істинним законом заломлення світла з правильною формулою для n.
29. Теорія райдуги
Припустімо, що промінь світла потрапляє до сферичної дощової краплини в якійсь точці P , утворюючи кут i з перпендикуляром до поверхні краплини в цій точці. Якби там не відбувалося заломлення, цей промінь світла продовжив би рухатися по прямій крізь краплину. У такому разі відрізок від центра краплини C до точки Q максимального наближення променя до центра утворив би прямий кут із променем світла, тому трикутник PCQ був би прямокутним із гіпотенузою, що дорівнює радіусу R краплі, та кутом у точці P , що дорівнює i (див. рис. 22a). Нехай прицільний параметр b буде відстанню максимального наближення незаломленого променя до центра, тобто довжиною сторони трикутника CQ , заданою за правилами елементарної тригонометрії:
b = R sin i .
Ми можемо однаково добре схарактеризувати окремі промені світла за відношенням b/R , як це робив Декарт, або ж за значенням кута падіння i .
Насправді ж через заломлення промінь входитиме до краплі під кутом r до перпендикуляра до поверхні, заданим законом заломлення:
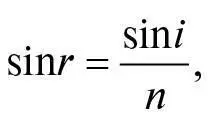
де n = 4/3 є відношенням швидкості світла в повітрі до його швидкості у воді. Промінь пройде крізь краплю й досягне її задньої поверхні у точці P ´. Оскільки відстані від центра краплі C до точок P та до P ´ однакові й дорівнюють радіусу R краплі, то трикутник із вершинами C, P та P ´ рівнобедрений, тому кути між променем світла та перпендикулярами до поверхні краплі в точках P та P ´ рівні й обидва дорівнюють r . Частина світла відбиватиметься від задньої поверхні краплі, і, за законом відбиття, кут між відбитим променем та перпендикуляром до поверхні в точці P ´ також дорівнюватиме r . Відбитий промінь перетинатиме краплю й ударятиме в її передню поверхню в точці P ´´, знову утворюючи кут r з перпендикуляром до поверхні в P ´´. Частина світла тоді виходитиме з краплини, і, за законом заломлення, кут між променем, що виходить, та перпендикуляром до поверхні в P ´´ дорівнюватиме первинному куту падіння i (див. рис. 22б, що демонструє шлях променя світла у площині, на якій лежать сам промінь, центр краплі та спостерігача. Лише ті промені, що стикаються з поверхнею краплини там, де вона перетинає цю площину, мають шанс досягти спостерігача).
Під час усіх цих відбиттів промінь світла відхилятиметься до центра краплі на кут i – r двічі – входячи до краплини й виходячи з неї, а також на кут 180° − 2 r , відбиваючись від задньої поверхні краплі, а отже, загальний кут відхилення променя становить:
2( i − r ) + 180° − 2 r = 180° − 4 r + 2 i .
Якби промінь світла відбивався від краплини назад у напрямі, протилежному напряму входу (тобто у випадку, коли i = r = 0), то цей кут дорівнював би 180°, а початкові та кінцеві напрямки променя світла були б паралельні, тому фактичний кут φ (фі) між початковими та кінцевими напрямками променями світла дорівнює:
Читать дальше

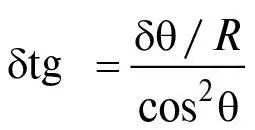
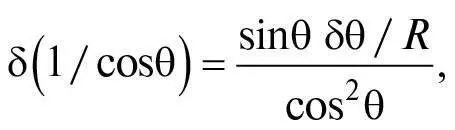
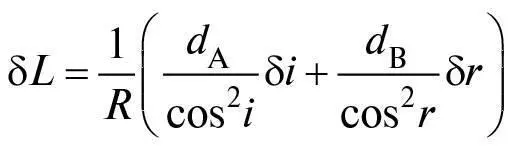
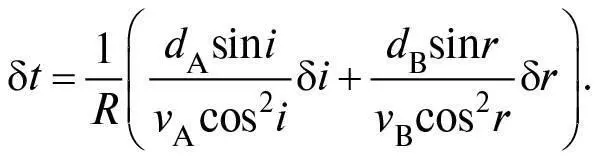
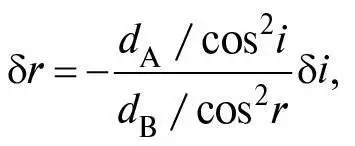
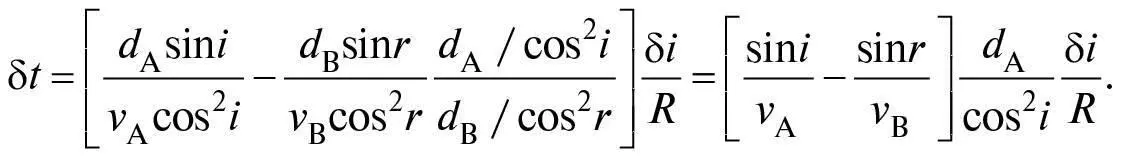
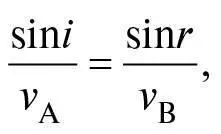
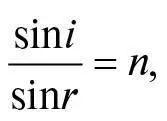
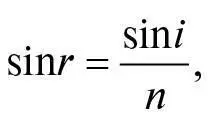





![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)




