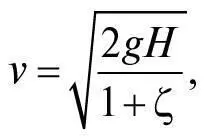
де g = 9,8 м/с2, а ζ (дзета) є відношенням енергії обертання кульки до її кінетичної енергії – числом, залежним від розподілу маси всередині кульки, що котиться. Для суцільної однорідної кульки ζ = 2/5. Це є також швидкістю кульки, коли вона вистрілює горизонтально в повітря з краю стільниці, тому горизонтальна відстань, яку проходить кулька за проміжок часу, за який вона впала на висоту h , дорівнюватиме:
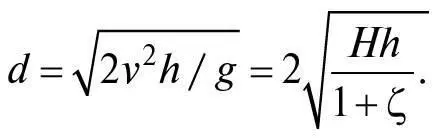
Ґалілей не згадував поправки на обертальний рух, вираженої ζ , але він, можливо, підозрював, що з огляду на якусь поправку пройдена горизонтальна відстань може бути менша, бо замість порівняння цієї відстані зі значенням 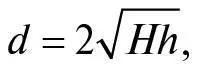 очікуваного, коли немає ζ, він лише перевірив, що для нерухомого столу з висотою h відстань d була фактично пропорційна
очікуваного, коли немає ζ, він лише перевірив, що для нерухомого столу з висотою h відстань d була фактично пропорційна 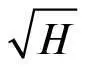 з точністю до кількох відсотків. Однак Ґалілей чомусь так і не опублікував результатів цього експерименту.
з точністю до кількох відсотків. Однак Ґалілей чомусь так і не опублікував результатів цього експерименту.
Щоб розв’язати багато астрономічних і математичних задач, зручно визначати параболу як граничний випадок еліпса, один фокус якого дуже віддалений від іншого. Рівняння для еліпса з великою віссю 2 a та малою віссю 2 b у технічній примітці 18 подано в такому вигляді:
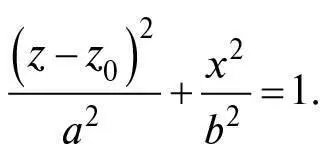
Для зручності подальших розрахунків ми замінили в ньому координати x та y , використовувані в технічній примітці 18, на z − z 0 та x , де z 0 – стала, яку можна вибрати довільно. Центр цього еліпса розташований у точці з координатами z = z 0 та x = 0. Як ми вже бачили в технічній примітці 18, фокус розташований у точці з координатами z − z 0 = − ae та x = 0, де e – ексцентриситет, який визначають з тотожності e 2 ≡ 1 − b 2/ a 2, а точка максимального наближення кривої до цього фокуса має координати z − z 0 = − a та x = 0. Буде зручно приписати цій точці максимального наближення координати z = 0 та x = 0, вибравши z 0 = а , у разі чого найближчий до неї фокус буде розташований у точці z = z 0 − ea = (1 − e ) a . Нам потрібно зробити а і b нескінченно великими, так щоб інший фокус віддалився до нескінченості і крива не мала максимальної координати x , але при цьому відстань (1 − e ) a максимального наближення до ближчого фокуса була скінченною, тому ми задаємо:
1 − e = l/a ,
де l залишається фіксованою, тоді як а прагне до нескінченості. Оскільки e наближається до одиниці при цій межі, мала піввісь b буде виражена формулою:
b 2 = a 2(1 − e 2) = a 2(1 − e )(1 + e ) → 2 a 2(1 − e ) = 2 la .
Якщо припустити, що z 0 = а , і використати цю формулу для b 2, отримаємо таке рівняння для еліпса:

Можемо відняти a 2/ a 2 з лівої частини рівняння і відповідно 1 з правої. Тоді множення залишків рівняння на а дає:

Для а , значно більшої за x, y або l , перший член можна прибрати, тож це рівняння набуває вигляду:
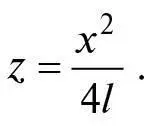
Це те саме, що рівняння, яке ми вивели для опису руху предмета, вистріленого горизонтально, за умови, якщо ми приймаємо, що
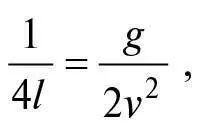
тому фокус F параболи розташований на відстані l = υ 2/2 g нижче від початкового положення вистріленого предмета (див. рис. 19).

Рис. 19.Параболічна траєкторія предмета, вистріленого з підвищення в горизонтальному напрямку. Точка F – це фокус цієї параболи.
Читать дальше

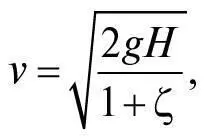
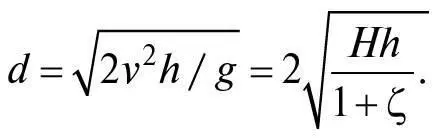
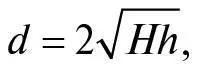 очікуваного, коли немає ζ, він лише перевірив, що для нерухомого столу з висотою h відстань d була фактично пропорційна
очікуваного, коли немає ζ, він лише перевірив, що для нерухомого столу з висотою h відстань d була фактично пропорційна 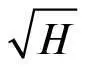 з точністю до кількох відсотків. Однак Ґалілей чомусь так і не опублікував результатів цього експерименту.
з точністю до кількох відсотків. Однак Ґалілей чомусь так і не опублікував результатів цього експерименту.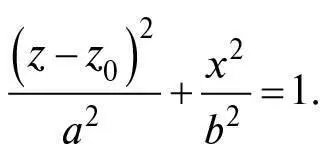


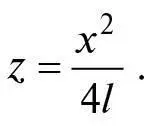
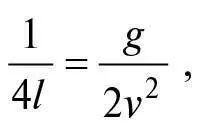






![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)




