Це є елементарним прикладом закону збереження енергії, що робить поняття енергії корисним у широкому різноманітті контекстів. Зокрема, закон збереження енергії демонструє важливість експериментів Ґалілея з кульками, що котилися донизу похилими площинами, для розв’язання задачі про вільне падіння, хоча сам Ґалілей цей аргумент не використовував. Для кульки масою m , що котиться донизу похилою площиною, кінетична енергія дорівнює mυ 2/2, де υ – швидкість уздовж цієї площини, а потенційна енергія дорівнює mgh , де h – знову висота. На додачу там є ще енергія обертання кульки, яку можна виразити так:
Еоберт 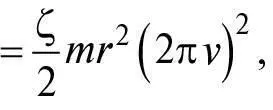
де r – радіус кульки, ν (ню) – кількість повних обертів кульки на секунду, а ζ (дзета) – величина, що залежить від форми кульки та розподілу маси всередині неї. У випадку суцільної однорідної кульки, яку, ймовірно, використовував у своїх експериментах Ґалілей, ζ = 2/5 (для порожнистої кульки ζ = 2/3.) Коли кулька робить один повний оберт, вона проходить відстань, що дорівнює її окружності 2π r , тому за час t , за який вона робить νt обертів, вона проходить відстань d = 2π r ν t , а отже, її швидкість дорівнює d/t = 2πν r . Використовуючи це у формулі для енергії обертання, отримаємо:
Еоберт 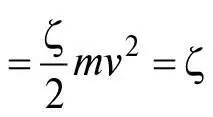 Екін.
Екін.
Поділивши це на m та на 1 + ζ, з огляду на закон збереження енергії отримаємо:
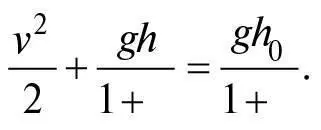
Це така сама залежність між швидкістю та пройденою відстанню d = h 0 – h , що має бути збережена для тіла, що падає вільно, крім того, що g замінене на g /(1 + ζ ). Не беручи до уваги цієї заміни, бачимо, що залежність швидкості кульки, що котиться донизу похилою площиною, від пройденої вертикальної відстані така сама, як і для тіла у вільному падінні. Отже, вивчаючи кульки, що котяться донизу похилими площинами, ми можемо довести, що тіла у вільному падінні рухаються з рівномірним прискоренням. Однак такий розрахунок не дає змоги виміряти прискорення, якщо тільки не брати до уваги множник 1/(1 + ζ ).
Унаслідок складних доведень Гюйґенс зумів показати, що час, потрібний маятнику довжиною L для коливання під невеличким кутом з одного боку до іншого, дорівнює:
τ = π 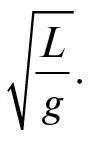
Тобто Гюйгенс показав, що цей час дорівнює π, помноженому на час, потрібний для падіння тіла на відстань d = L /2.
26. Параболічні траєкторії
Припустімо, що якийсь предмет вистрілили горизонтально зі швидкістю υ . Нехтуючи опором повітря, він продовжуватиме летіти горизонтально з однаковою швидкістю, але водночас прискорюватиметься донизу. Отже, за час t він подолає горизонтальну відстань x = υt та вертикальну відстань z , пропорційну квадрату часу, тобто z = gt 2/2, де g = 9,8 м/с2 (стала, яку вже після смерті Ґалілея виміряв Гюйґенс). Враховуючи, що t = x / υ , маємо:
z = gx 2/2 v 2.
Це рівняння, задаючи одну координату пропорційною квадрату іншої, визначає параболу.
Зверніть увагу: якщо цей предмет вистрілили з гармати на висоті h над землею, то горизонтальна відстань x , пройдена, коли предмет пролетить відстань z = h і досягне землі, дорівнює 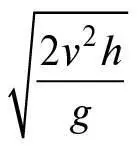 . Навіть не знаючи υ або g , Ґалілей міг підтвердити, що шляхом предмета є парабола, вимірюючи пройдену відстань d для різноманітних висот падіння h , а також перевіряючи, що d пропорційна квадратному кореню з h . Точно невідомо, чи зробив це колись Ґалілей, але є свідчення, що в 1608 році він провів дуже схожий експеримент, стисло згаданий у розділі 12. Кулька в ньому котилася донизу похилою площиною з різноманітних початкових висот H , потім котилася вздовж горизонтальної стільниці, на якій була встановлена ця похила площина, і нарешті вистрілювала в повітря з краю столу. Як показано в технічній примітці 25, швидкість кульки внизу похилої площини дорівнює:
. Навіть не знаючи υ або g , Ґалілей міг підтвердити, що шляхом предмета є парабола, вимірюючи пройдену відстань d для різноманітних висот падіння h , а також перевіряючи, що d пропорційна квадратному кореню з h . Точно невідомо, чи зробив це колись Ґалілей, але є свідчення, що в 1608 році він провів дуже схожий експеримент, стисло згаданий у розділі 12. Кулька в ньому котилася донизу похилою площиною з різноманітних початкових висот H , потім котилася вздовж горизонтальної стільниці, на якій була встановлена ця похила площина, і нарешті вистрілювала в повітря з краю столу. Як показано в технічній примітці 25, швидкість кульки внизу похилої площини дорівнює:
Читать дальше

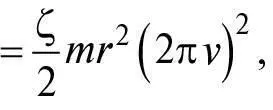
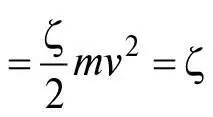 Екін.
Екін.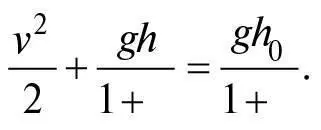
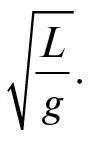
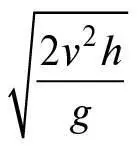 . Навіть не знаючи υ або g , Ґалілей міг підтвердити, що шляхом предмета є парабола, вимірюючи пройдену відстань d для різноманітних висот падіння h , а також перевіряючи, що d пропорційна квадратному кореню з h . Точно невідомо, чи зробив це колись Ґалілей, але є свідчення, що в 1608 році він провів дуже схожий експеримент, стисло згаданий у розділі 12. Кулька в ньому котилася донизу похилою площиною з різноманітних початкових висот H , потім котилася вздовж горизонтальної стільниці, на якій була встановлена ця похила площина, і нарешті вистрілювала в повітря з краю столу. Як показано в технічній примітці 25, швидкість кульки внизу похилої площини дорівнює:
. Навіть не знаючи υ або g , Ґалілей міг підтвердити, що шляхом предмета є парабола, вимірюючи пройдену відстань d для різноманітних висот падіння h , а також перевіряючи, що d пропорційна квадратному кореню з h . Точно невідомо, чи зробив це колись Ґалілей, але є свідчення, що в 1608 році він провів дуже схожий експеримент, стисло згаданий у розділі 12. Кулька в ньому котилася донизу похилою площиною з різноманітних початкових висот H , потім котилася вздовж горизонтальної стільниці, на якій була встановлена ця похила площина, і нарешті вистрілювала в повітря з краю столу. Як показано в технічній примітці 25, швидкість кульки внизу похилої площини дорівнює:




![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)




