β = θ – α = (1 – 1/ n )θ.
Це кут між променем світла та перпендикуляром до пласкої задньої поверхні лінзи, коли промінь світла досягає цієї поверхні. З другого боку, коли промінь світла виходить крізь задню поверхню лінзи, він утворює інший кут – ϕ (фі) – з перпендикуляром до цієї поверхні. Співвідношення між ϕ та β таке саме, як тоді, коли світло йшло б у протилежному напрямку: у такому разі ϕ був би кутом падіння, а β – кутом заломлення, тож β = ϕ /n , а отже:
ϕ = n β = ( n − 1)θ.
З цього видно, що ϕ прямо пропорційний θ, а отже, використовуючи нашу попередню формулу для f/r , отримуємо:
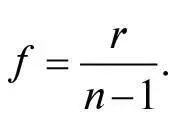
Ця рівність не залежить від θ, тому, як і обіцяно, усі горизонтальні промені світла, що входять до лінзи, збігаються в одній точці на осьовій лінії лінзи.
Якщо радіус кривини r дуже великий, то кривина передньої поверхні лінзи дуже мала, а тому лінза працює майже так само, як пласке скельце, тобто заломлення світла на вході до лінзи майже компенсоване його заломленням на виході з лінзи. Також незалежно від форми лінзи, якщо показник заломлення n близький до 1, то лінза заломлює промінь світла дуже мало. В обох цих випадках фокусна відстань дуже велика, і тоді ми називаємо лінзу слабкою. Сильна лінза – це та, що має помірний радіус кривини й показник заломлення, помітно відмінний від 1 (як, наприклад, лінза зі скла, для якої n = 1,5).
Подібний результат отримаємо й у разі, якщо задня поверхня лінзи не пласка, а є сегментом сфери радіусом r ´. Тоді фокусна відстань дорівнює:
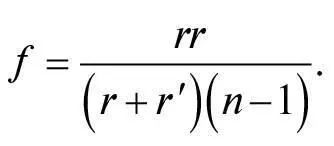
Це дає нам такий самий результат, що й раніше, якщо r ´ значно більше за r , тобто задня поверхня лінзи майже плоска.
Поняття фокусної відстані можна також поширити на увігнуту лінзу на кшталт тієї, яку Ґалілей використовував як окуляр свого телескопа. Увігнута лінза може заломлювати промені світла, що збігаються в одну точку, так, щоб вони були паралельні чи навіть розбігалися в різні боки. Ми можемо визначити фокусну відстань такої лінзи, розглядаючи промені світла, що збігаються, які лінза робить паралельними; фокусною відстанню в такому разі буде відстань точки позаду лінзи, до якої такі промені збігалися б, якби лінза не робила їх паралельними. Хоча її суть інша, фокусна відстань увігнутої лінзи задають формулою, аналогічною тій, яку ми вже вивели для опуклої лінзи.
23. Телескопи
Як ми вже бачили в технічній примітці 22, тонка опукла лінза фокусуватиме промені світла, які на неї падають паралельно її центральній осі, у точці F на цій осі, на певній відстані позаду лінзи, яку називають фокусною відстанню f цієї лінзи. Паралельні промені світла, що падають на лінзу під невеликим кутом γ (гамма) до центральної осі, також фокусуватимуть лінзою, але в точці, трохи зміщеній відносно центральної осі. Щоб зрозуміти, наскільки вона зміщена, ми можемо уявити собі поворот шляху променя світла на рис. 16a навколо лінзи на кут γ. Тоді відстань d фокуса від центральної осі лінзи відноситиметься до окружності кола радіусом f , як γ до 360°:
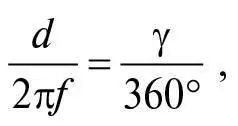
а отже:
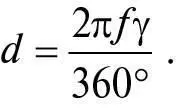
(Це працює лише для тонкої лінзи; інакше d також залежить від кута θ, поданого в технічній примітці 22.) Якщо промені світла від якогось далекого об’єкта падають на лінзу під кутами, значення яких лежать у межах діапазону Δγ (дельта гамма), вони фокусуватимуться на відрізку висотою Δ d , заданою формулою:
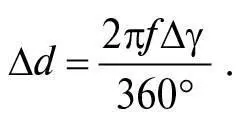
(Як і зазвичай, ця формула простіша, якщо Δγ вимірюють у радіанах, що дорівнюють 360°/2π, а не у градусах; у цьому разі вона матиме вигляд Δ d = f Δγ.) Цей відрізок сфокусованого світла називають уявним зображенням (див. рис. 17a).
Ми не можемо побачити уявного зображення, просто подивившись на нього, бо після утворення цього зображення промені світла розбігаються знову.
Щоб сфокусуватися в точці на сітківці розслабленого людського ока, промені світла мають увійти до кришталика ока в більш-менш паралельних напрямках. Телескоп Кеплера містив другу опуклу лінзу, яку називають окуляром, що давала змогу фокусувати промені світла, які розбігаються від уявного зображення так, щоб вони виходили з телескопа в паралельних напрямках. Міркуючи так само, але щодо променів світла зі зворотними напрямками, ми побачимо, що для того, щоб промені від якоїсь точки на джерелі світла виходили з телескопа в паралельних напрямках, окуляр має бути розташований на відстані f ´ від уявного зображення, де f ´ – фокусна відстань окуляра (див. рис. 17б). Тобто довжина телескопа L має дорівнювати сумі фокусних відстаней:
Читать дальше

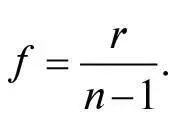
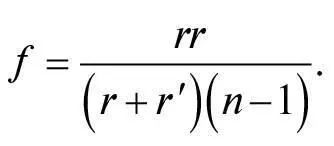
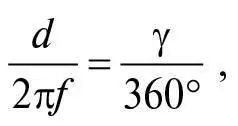
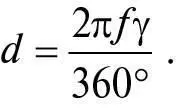
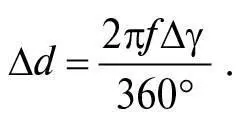





![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)




