Розгляньмо вертикальну скляну лінзу з опуклою поверхнею спереду та пласкою ззаду, схожу на ту, що її Ґалілей та Кеплер використовували в передній частині своїх телескопів. Криві поверхні, найзручніші для виточування та шліфування, є сегментами сфер, тож ми припускатимемо, що опукла передня сторона лінзи є сегментом сфери радіусом r . Ми також вважатимемо, що ця лінза тонка, тобто її максимальна товщина значно менша за r .
Припустімо, що якийсь промінь світла, який рухається в горизонтальному напрямку, паралельному осі лінзи, падає на лінзу в точці P , при цьому відрізок від центра кривини C (позаду лінзи) до точки P утворює з осьовою лінією лінзи кут θ (тета). Лінза заломить цей промінь світла так, що коли він вийде ззаду неї, то утворить з осьовою лінією лінзи інший кут – ϕ. Зрештою промінь перетинається з осьовою лінією лінзи в якійсь точці F (див. рис. 16a). Нам потрібно обчислити відстань f , на яку ця точка віддалена від задньої поверхні лінзи, і показати, що вона не залежить від θ, а тому всі горизонтальні промені світла, які падають на лінзу, перетинають осьову лінію лінзи в тій самій точці F . Отже, можемо сказати, що світло, яке проходить крізь лінзу, фокусується в точці F , а відстань f цієї точки від лінзи є фокусною відстанню лінзи.
Насамперед зверніть увагу, що довжина дуги на передньому боці лінзи від осьової лінії до точки P є часткою θ/360° всієї окружності 2π r кола радіусом r . З другого боку, та сама дуга становить ϕ/360° всієї окружності 2π f кола радіусом f . Оскільки ці дуги однакові, маємо:
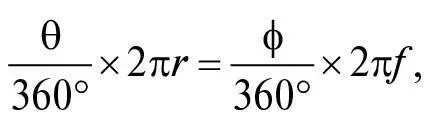
а отже, скоротивши 360° та 2π, отримуємо:
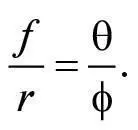
Тому, щоб обчислити фокусну відстань, нам потрібно обчислити відношення ϕ до θ.
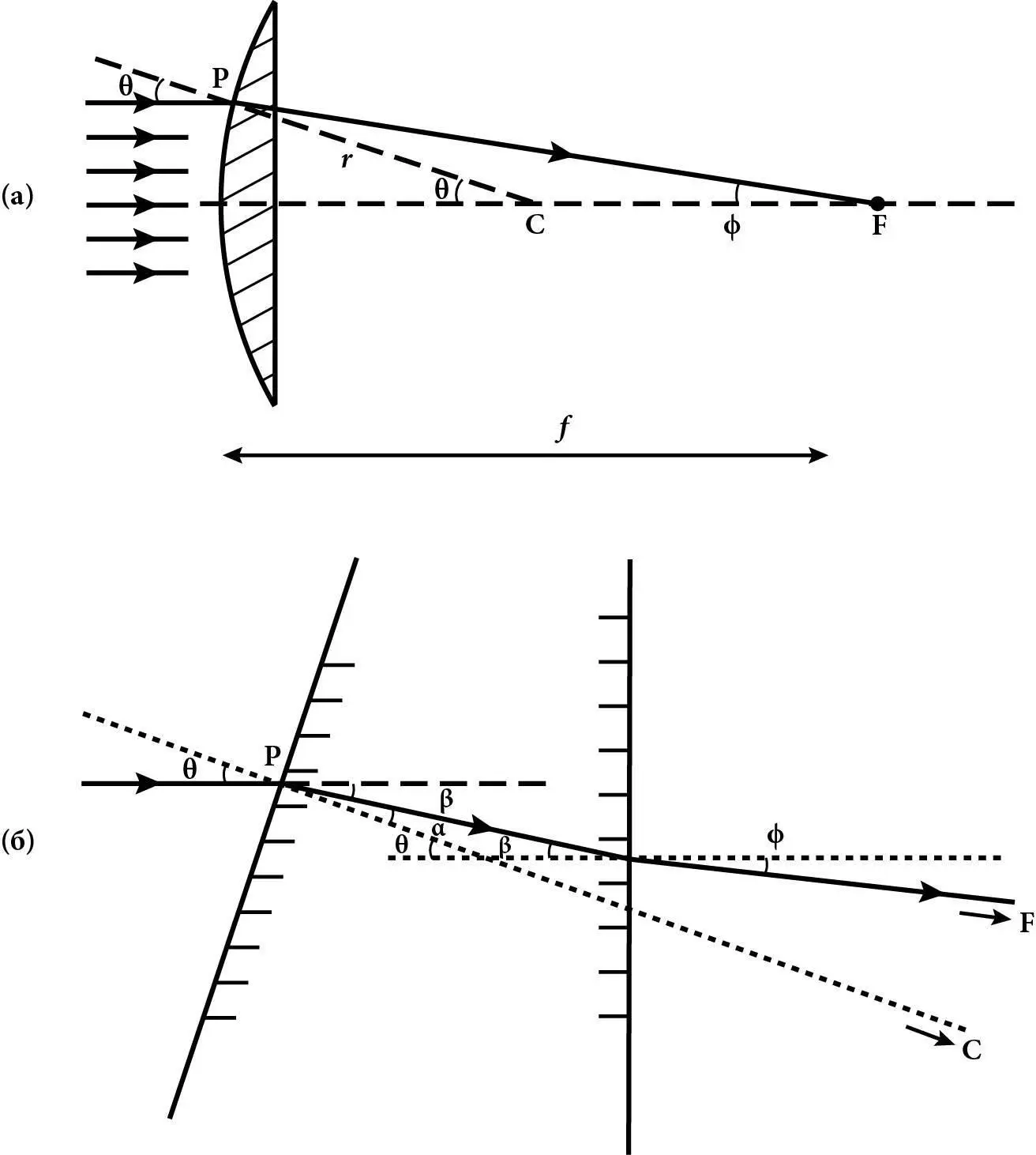
Рис. 16.Фокусна відстань: a) визначення фокусної відстані. Горизонтальна пунктирна лінія – це вісь лінзи. Горизонтальні лінії, позначені стрілками, позначають промені світла, що входять у лінзу паралельно до цієї осі. Один промінь показаний таким, що входить до лінзи в точці P, де він утворює невеликий кут θ з перпендикулярною до сферичної поверхні прямою, що проходить через центр кривини C і точку P. Цей промінь заломлюється лінзою, утворюючи кут ϕ з віссю лінзи й перетинаючи вісь у фокусній точці F на відстані f від лінзи. Це і є фокусна відстань. Кут ϕ пропорційний куту θ, тому всі горизонтальні промені фокусуються в точці F; б) обчислення фокусної відстані. Тут показана невеличка частина лінзи, де похила суцільна лінія зі штрихуванням (зліва) означає маленький сегмент опуклої поверхні лінзи. Суцільна лінія, позначена стрілкою, показує шлях променя світла, що входить до лінзи в точці P, де утворює невеличкий кут θ з перпендикуляром до випуклої поверхні в цій точці. Цей перпендикуляр зображений похилою пунктирною лінією, що є частиною прямої, яка проходить через точку P і центр кривизни лінзи С, розташований за межами цього рисунку. Усередині лінзи цей промінь заломлюється так, що утворює кут α з цим перпендикуляром, а на виході з лінзи заломлюється знову так, що утворює кут ϕ з перпендикуляром до плоскої задньої поверхні лінзи. Цей перпендикуляр зображено пунктирною лінією, паралельною до осі лінзи.
Для цього зауважмо, що відбувається з променем світла всередині лінзи (див. рис. 16б). Відрізок від центра кривини C до точки P , де горизонтальний промінь світла вдаряє в лінзу, перпендикулярний опуклій сферичній поверхні лінзи в точці P , тому кут між цим перпендикуляром та променем світла (тобто кут падіння) дорівнює θ. Як було відомо ще Клавдію Птолемею, якщо θ малий (як це буде в разі тонкої лінзи), то кут α (альфа) між променем світла всередині скла та зазначеним перпендикуляром (тобто кут заломлення) буде пропорційний куту падіння:
α = θ/ n ,
де n > 1 є сталою, відомою як показник заломлення, що залежить від властивостей скла та довкілля, зазвичай повітря. (Ферма показав, що n – це швидкість світла в повітрі, поділена на швидкість світла у склі, але ця інформація тут не має значення.) Тоді кут β (бета) між променем світла всередині скла та осьовою лінією лінзи дорівнює:
Читать дальше

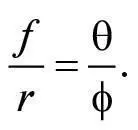






![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)




