Стивен Вайнберг - Пояснюючи світ

W спр − W поз = W вит,

де W вит – вага води, витісненої підвішеним тілом. Тому, зважуючи тіло за підвішування у воді та поза водою, можна знайти як W поз, так і W спр, і так знайти W вит. Якщо тіло має об’єм V , то

W вит = ρводи V

де ρводи (роводи) – густина (вага на об’єм) води, близька до значення 1 г/см3. (Звісно, для тіла простої форми, наприклад куба, ми могли би знайти V , просто вимірюючи розміри тіла, але для тіла неправильної форми, як-от корона, це доволі складно.) Крім того, справжня вага тіла становить:

W спр = ρтіла V ,

де ρтіла – густина тіла. За співвідношення W спр та W вит об’єм скорочується, тому з вимірювань W поз та W спр можна знайти співвідношення густин тіла та води:

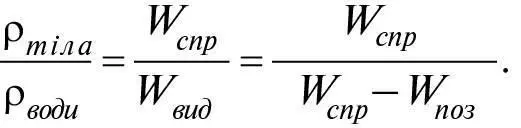
Таке співвідношення називають відносною густиною матеріалу, з якого складається тіло. Наприклад, якщо якесь тіло важить у воді на 20 % менше, ніж у повітрі, то W спр − W поз = 0,20 × W спр, тому його густина має бути у 1/0,2 = 5 разів більша за густину води. Тобто його відносна густина дорівнює 5.

У цьому аналізі з водою не пов’язано нічого особливого; якби такі самі вимірювання проводили для якогось тіла, підвішеного в якійсь іншій рідині, то відношення справжньої ваги цього тіла до зменшення його ваги під час підвішування в цій рідині дорівнювало б відношенню густини цього тіла до густини цієї рідини. За цим принципом тіло відомої ваги та об’єму використовують, щоб вимірювати густини різних рідин, у які це тіло занурюють.

10. Площі кіл

Щоб обчислити площу якогось кола, Архімед уявляв собі описаний навколо цього кола багатокутник із великою кількістю сторін. Для простоти розуміння розгляньмо правильний багатокутник, усі сторони та кути якого рівні. Площа цього багатокутника є сумою площ усіх прямокутних трикутників, утворених проведенням ліній від центра до вершин цього багатокутника, а також ліній від центра до середин сторін багатокутника (див. рис. 4, на якому цей багатокутник представлений правильним восьмикутником). Площа прямокутного трикутника дорівнює половині добутку двох його катетів, бо два такі трикутники можна скласти по їхніх гіпотенузах, утворивши прямокутник, площа якого дорівнює добутку його сторін (що є катетами таких трикутників). У нашому випадку це означає, що площа кожного трикутника дорівнює половині добутку відстані r до середини сторони (яка є саме радіусом кола) і відстані s від середини сторони до найближчої вершини багатокутника, яка, звісно, дорівнює половині довжини цієї сторони багатокутника. Додаючи всі ці площі, ми знаходимо, що площа всього багатокутника дорівнює добутку половини r на повний периметр багатокутника. Якщо збільшувати кількість сторін багатокутника до нескінченності, його площа наближатиметься до площі вписаного в нього кола, а його периметр наближатиметься до окружності кола. Тому площа кола дорівнює добутку половини його окружності на його радіус.

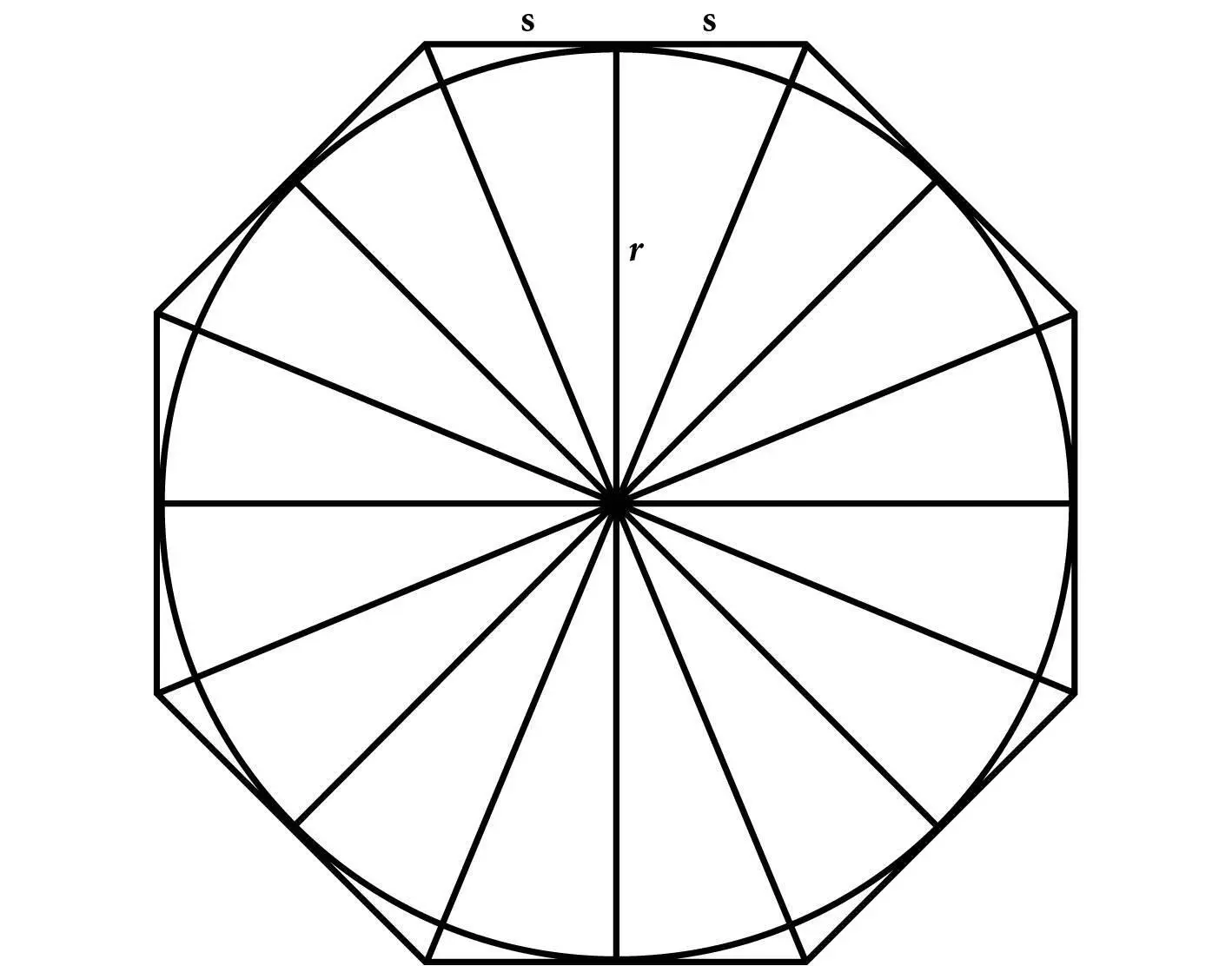
Рис. 4.Обчислення площі кола. У цьому обчисленні багатокутник з багатьма сторонами описаний навколо кола. Тут багатокутник має вісім сторін, а його площа вже близька до площі кола. Що більша кількість сторін багатокутника, то ближча стає його площа до площі кола.

Говорячи сучасною мовою, ми визначаємо число π = 3,14159… так, що окружність кола з радіусом r дорівнює 2π r . Площа кола, отже, дорівнює

1/2 × r × 2π r = π r 2.

Те саме справедливо і для вписаного в коло багатокутника, а не описаного, як зображено на рис. 4. Оскільки це коло завжди розташоване між зовнішнім багатокутником, описаним навколо нього, і внутрішнім багатокутником, вписаним усередину нього, обчислюючи площі багатокутників обох типів, Архімед зміг відобразити верхню та нижню границі для відношення окружності кола до його радіуса, тобто для 2π.

11. Розміри Сонця й Місяця та відстані до них

Арістарх використовував для визначення відстаней від Землі до Сонця й Місяця, а також діаметрів Сонця й Місяця дані чотирьох спостережень, виразивши результати в діаметрах Землі. Розгляньмо кожне з цих спостережень по черзі й подивімося, що можна з них дізнатися. Нехай відстані від Землі до Сонця та Місяця будуть позначені як d с та d м відповідно; а діаметри Сонця, Місяця та Землі як D с, D м і D з. Припустімо, що ці діаметри незначні проти відстаней, тому, міркуючи про відстані від Землі до Місяця або Сонця, можемо не зазначати точки на Землі, Місяці або Сонці, з яких вимірюють відстані.