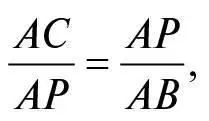
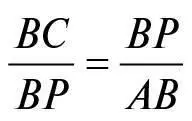
Звідси випливає, що AP 2 = AC × AB , а BP 2 = ВС × AB . Додавання цих двох рівнянь дає
AP 2 + BP 2 = ( AC + ВС ) × AB.
Але AC + ВС = AB, що й треба було довести.
5. Ірраціональні числа
Давньогрецькі математики знали лише раціональні числа. Це числа, що є або цілими, як-от 1, 2, 3 і далі, або співвідношеннями цілих (1/2, 2/3 тощо). Якщо співвідношення довжин двох відрізків є раціональним числом, то такі відрізки вважали «порівнянними». Наприклад, якщо співвідношення становить 3/5, це означало, що один відрізок, узятий п’ять разів, має таку саму довжину, як другий, узятий три рази. Тому давньогрецькі математики були, напевно, шоковані, усвідомивши, що не всі лінії сумірні. Зокрема, у прямокутному рівнобедреному трикутнику гіпотенуза несумірна з жодною із двох рівних сторін. Говорячи сучасною мовою, оскільки, згідно з теоремою Піфагора, квадрат гіпотенузи такого трикутника дорівнює подвоєному квадрату довжини будь-якої з двох рівних сторін, то довжина гіпотенузи дорівнює довжині будь-якої з інших сторін, помноженій на квадратний корінь із 2. Тож квадратний корінь із 2 не є раціональним числом. Доведення цього Евклід подає у Книзі X «Начал». Він спирається на припущення протилежного – що є якесь раціональне число, квадратом якого є 2, – а потім доводить абсурдність цього.
Припустімо, що якесь раціональне число p/q (де p та q – цілі числа) має квадрат, що дорівнює 2:
( p/q )2 = 2.
Тоді існуватиме нескінченна кількість таких пар чисел, отримуваних множенням будь-яких заданих p та q на будь-які рівні цілі числа, але припустімо, що p та q – найменші цілі числа, для яких ( p/q )2 = 2. З цього рівняння випливає:
p 2 = 2 q 2.
З цього видно, що p 2 є парним числом, але добуток будь-яких двох непарних чисел непарний, тому число p має бути тільки парне. Тобто ми можемо написати p = 2 p ´, де p ´ – ціле число. Але тоді
q 2 = 2 p ´2,
тому, за тою самою логікою, число q також парне, а отже, його можна виразити як q = 2 q ´, де q ´ – ціле число. Але тоді p/q = p ´ /q ´, тому
( p ´ /q ´)2 = 2,
де p ´ та q ´ – цілі числа, які відповідно вдвічі менші за p та q , усупереч визначенню p та q як найменших цілих чисел, для яких справедлива рівність ( p/q )2 = 2. Отже, первинне припущення, що є цілі числа p та q , для яких ( p/q )2 = 2, веде до суперечності, тож такі числа не можуть існувати.
Ця теорема веде до очевидного узагальнення: будь-яке число на кшталт 3, 5, 6 тощо, що не є саме квадратом якогось цілого числа, не може бути квадратом якогось раціонального числа. Наприклад, якщо 3 = ( p/q )2, де p та q – найменші цілі числа, за яких буде збережена ця рівність, тоді p 2 = 3 q 2, але це неможливо, якщо тільки ми не маємо p = 3 p ´ для якогось цілого числа p ´, але тоді q 2 = 3 p ´2, тому q = 3 q ´, для якогось цілого числа q , тому 3 = ( p ´ /q ´)2, усупереч твердженню, що p та q – найменші цілі числа, для яких справедлива рівність p 2 = 3 q 2. Отже, усі квадратні корені з 3, 5, 6… є ірраціональними числами.
У сучасній математиці ми визнаємо існування таких ірраціональних чисел, як число, позначене √2, квадратом якого є 2. Якщо зобразити такі числа як десятковий дріб, то послідовність знаків після коми в ньому триватиме нескінченно й без повторень; наприклад, √2 = 1,414215562… Послідовності як раціональних, так і ірраціональних чисел однаково нескінченні, але в певному сенсі ірраціональних чисел значно більше, ніж раціональних, бо раціональні числа можна перерахувати в нескінченній послідовності, що містить будь-яке задане раціональне число:
1, 2, 1/2, 3, 1/3, 2/3, 3/2, 4, 1/4, 3/4, 4/3, …,
тоді як скласти перелік усіх ірраціональних чисел жодним чином неможливо.
6. Гранична швидкість
Щоб зрозуміти, як спостереження тіл, що падають, могли привести Арістотеля до його ідей про рух, ми можемо скористатися фізичним принципом, невідомим Арістотелю, – другим законом Ньютона. Згідно з цим законом, прискорення a якогось тіла (темп, з яким зростає його швидкість) дорівнює повній рівнодійній силі F , що діє на тіло, поділеній на масу цього тіла m :
Читать дальше

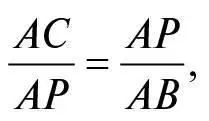
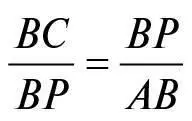





![Стивен Вайнберг - Первые три минуты [litres]](/books/398000/stiven-vajnberg-pervye-tri-minuty-litres-thumb.webp)




