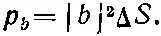 (2.10)
(2.10)
Когда же имеются две частицы, то вероятность рассеяния а в dS 1и b в dS 2будет
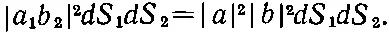 (2.11)
(2.11)
Если нам нужна вероятность того, что обе частицы (и а , и b ) попали в счетчик, мы должны будем проинтегрировать dS 1и dS 2по всей площади Δ S ; получится
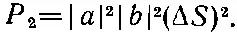
Заметим, кстати, что это равно просто р а · р b в точности так, как если бы мы предположили, что частицы а и b действуют независимо друг от друга.
Однако, когда две частицы тождественны, имеются две неразличимые возможности для каждой пары элементов поверхности dS 1и dS 2. Частица а , попадающая в dS 2, и частица b , попадающая в dS 1, неотличимы от а в dS 1и от b в dS 2, так что амплитуды этих процессов будут интерферировать. (Когда у нас были две различные частицы, то, хотя мы на самом деле не заботились о том, какая из них куда попадает в счетчике, мы все же в принципе могли это узнать; так что интерференции не было. А для тождественных частиц мы и в принципе не можем этого сделать.) Мы должны тогда написать, что вероятность того, что пара частиц очутится в dS 1и dS 2, есть
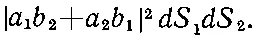 (2.13)
(2.13)
Однако сейчас, интегрируя по поверхности счетчика, нужно быть осторожным. Пустив dS 1и dS 2странствовать по всей площади Δ S , мы бы сосчитали каждую часть площади дважды , поскольку в (2.13) входит все, что может случиться [4] Перестановка dS 1 и dS 2 в (2.11) приводит к другому событию, так что оба элемента поверхности обязаны пройтись по всей площади счетчика. В (2.13) мы рассматриваем dS 1 и dS 2 как пару и включаем все, что может случиться. Если интегралы опять включают все, что случится, когда dS 1 и dS 2 поменяются местами, то все считается дважды.
с каждой парой элементов поверхности dS 1и dS 2. Но интеграл можно все равно подсчитать, если учесть двукратный счет, разделив результат пополам. Тогда мы получим, что Р 2для тождественных бозе-частиц есть
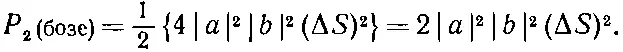 (2.14)
(2.14)
И опять это ровно вдвое больше того, что мы получили в (2.12) для различимых частиц.
Если вообразить на мгновение, что мы откуда-то знали, что канал b уже послал свою частицу в своем направлении, то можно сказать, что вероятность того, что вторая частица направится в ту же сторону, вдвое больше того, чего можно было бы ожидать, если бы мы посчитали это событие независимым. Таково уж свойство бозе-частиц, что если есть одна частица в каких-то условиях, то вероятность поставить в те же условия вторую вдвое больше, чем если бы первой там не было. Этот факт часто формулируют так: если уже имеется одна бозе-частица в данном состоянии, то амплитуда того, что туда же, ей на голову, можно будет поместить вторую, в √2 раз больше, чем если бы первой там не было. (Это неподходящий способ формулировать результат с той физической точки зрения, какую мы избрали, но, если это правило последовательно применять, оно все же приводит к верному результату.)
§ 3. Состояния с n бозе-частицами
Распространим наш результат на тот случай, когда имеются n частиц. Вообразим случай, изображенный на фиг. 2.4.
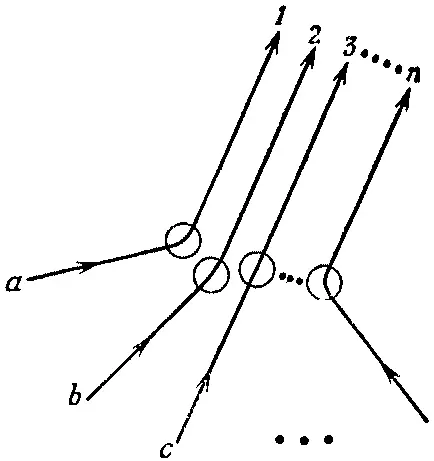
Фиг. 2.4. Рассеяние n частиц в близкие конечные состояния.
Есть n частиц а, b, с , ..., которые рассеиваются в направлениях 1, 2, 3, ..., n . Все n направлений смотрят в небольшой счетчик, который стоит где-то поодаль. Как и в предыдущем параграфе, выберем нормировку всех амплитуд так, чтобы вероятность того, что каждая частица, действуя по отдельности, попадет в элемент поверхности dS счетчика, была равна
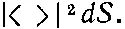
Сперва предположим, что частицы все различимы, тогда вероятность того, что n частиц будут одновременно зарегистрированы в n разных элементах поверхности, будет равна
Читать дальше

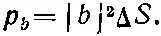 (2.10)
(2.10)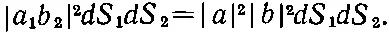 (2.11)
(2.11)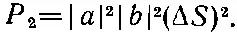
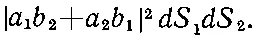 (2.13)
(2.13)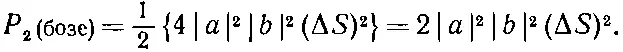 (2.14)
(2.14)
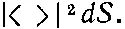



![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


