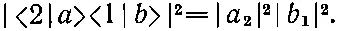
Представим себе теперь, что имеется пара крошечных счетчиков, которые ловят рассеянные частицы. Вероятность Р 2того, что они засекут сразу обе частицы, равна просто
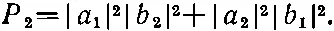 (2.3)
(2.3)
Положим теперь, что направления 1 и 2 очень близки. Будем считать, что а с изменением направления меняется плавно, тогда а 1и а 2при сближении направлений 1 и 2 должны приближаться друг к другу. При достаточном сближении амплитуды а 1и а 2сравняются, и можно будет положить а 1= а 2и обозначить каждую из них просто а ; точно так же мы положим и b 1= b 2= b . Тогда получим
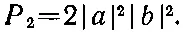 (2.4)
(2.4)
Теперь, однако, предположим, что а и b — тождественные бозе-частицы. Тогда процесс перехода а в состояние 1, а b в состояние 2 нельзя будет отличить от обменного процесса, в котором b переходит в 2, а а — в 1. В этом случае амплитуды двух различных процессов могут интерферировать. Полная амплитуда того, что в каждом из счетчиков появится по частице, равна
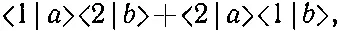 (2.5)
(2.5)
и вероятность того, что ими будет зарегистрирована пара, дается квадратом модуля этой амплитуды:
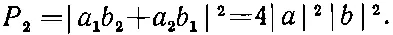 (2.6)
(2.6)
В итоге выясняется, что вдвое более вероятно обнаружить две идентичные бозе-частицы, рассеянные в одно и то же состояние, по сравнению с расчетом, проводимым в предположении, что частицы различны .
Хотя мы считали, что частицы наблюдаются двумя разными счетчиками, — это несущественно. В этом можно убедиться следующим образом. Вообразим себе, что оба направления 1 и 2 привели бы частицы в один и тот же маленький счетчик, который находится на каком-то расстоянии. Мы определим направление 1, говоря, что оно смотрит в элемент поверхности dS 1счетчика. Направление же 2 смотрит в элемент поверхности dS 2счетчика. (Считается, что счетчик представляет собой поверхность, поперечную к линии рассеяния.) Теперь уже нельзя говорить о вероятности того, что частица направится точно в каком-то направлении или в определенную точку пространства. Это невозможно — шанс зарегистрировать любое фиксированное направление равен нулю. Если уж нам хочется точности, то нужно так определить наши амплитуды, чтобы они давали вероятность попадания на единицу площади счетчика. Пусть у нас была бы только одна частица a ; она бы имела определенную амплитуду рассеяния в направлении 1. Пусть<1| а >= a 1определяется как амплитуда того, что а рассеется в единицу площади счетчика, расположенного в направлении 1. Иными словами, мы выбираем масштаб а 1и говорим, что она «нормирована» так, что вероятность того, что а рассеется в элемент площади dS 1равна
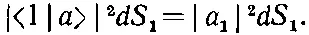 (2.7)
(2.7)
Если вся площадь нашего счетчика Δ S и мы заставим dS 1странствовать по этой площади, то полная вероятность того, что частица а рассеется в счетчик, будет
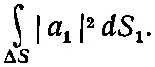 (2.8)
(2.8)
Как и прежде, мы хотим считать счетчик настолько малым, что амплитуда а 1на его поверхности не очень меняется; значит, а 1будет постоянным числом, и мы обозначим его через а . Тогда вероятность того, что частица а рассеялась куда-то в счетчик, равна
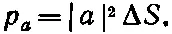 (2.9)
(2.9)
Таким же способом мы придем к выводу, что частица b (когда она одна) рассеивается в элемент площади dS 2с вероятностью
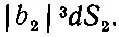
(Мы говорим d S 2, а не dS 1в расчете на то, что позже частицам а и b будет разрешено двигаться в разных направлениях.) Опять положим b 2равным постоянной амплитуде b ; тогда вероятность того, что частица b будет зарегистрирована счетчиком, равна
Читать дальше

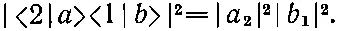
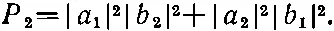 (2.3)
(2.3)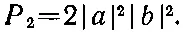 (2.4)
(2.4)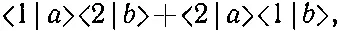 (2.5)
(2.5)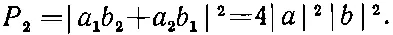 (2.6)
(2.6)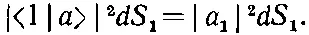 (2.7)
(2.7)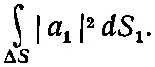 (2.8)
(2.8)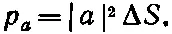 (2.9)
(2.9)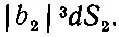



![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


