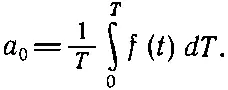 (50.3)
(50.3)
Найти остальные коэффициенты ненамного труднее. Чтобы сделать это, используем один фокус, открытый самим Фурье. Предположим, что мы умножили обе стороны уравнения (50.2) на какую-то гармоническую функцию, скажем на cos7ω t . При этом получается
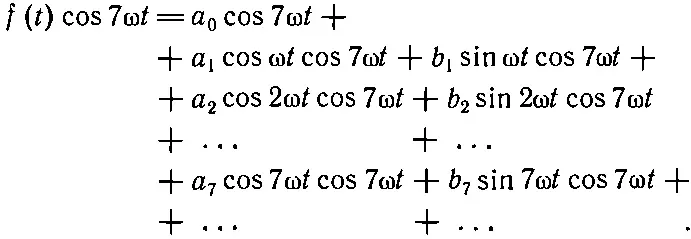 (50.4)
(50.4)
А теперь усредним обе стороны равенства. Среднее от члена a 0cos7ωt по периоду Т пропорционально среднему от косинуса по семи его периодам. Но последнее просто равно нулю. Среднее почти всех остальных членов тоже будет равно нулю. Действительно, давайте рассмотрим член с а 1. Мы знаем, что в общем случае
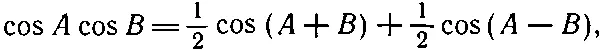 (50.5)
(50.5)
так что член с а 1равен
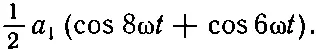 (50.6)
(50.6)
Таким образом получаются два косинуса: один с восемью полными периодами, а другой с шестью. Оба они равны нулю . Поэтому среднее значение этого члена тоже равно нулю.
Для члена с а 2мы получаем cos9ωt и cos5ωt, каждый из которых при усреднении превратится в нуль. Для члена с а 9получится cos16ωt и cos(-2ω t ). Но cos(-2ωt) — это то же самое, что cos2ωt, так что опять оба члена дадут при усреднении нуль. Ясно, что все слагаемые с косинусами, за исключением одного, дадут при усреднении нуль. Этим единственным слагаемым будет член с а 7. Для него же мы получим
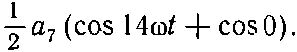 (50.7)
(50.7)
Косинус нуля равен единице, а среднее от него, разумеется, тоже равно единице. Итак, мы получили, что среднее от всех членов с косинусами уравнения (50.4) равно 1/ 2а 7.
Еще легче расправиться с синусами. Когда мы умножаем их накосинус типа cos n ω t , то таким же методом можно показать, что все они при усреднении обращаются в нуль.
Мы видим, что способ, придуманный Фурье, действует как своеобразное сито. Когда мы умножаем на cos7ωt и усредняем, то все члены, кроме а 7, отсеиваются и в результате остается
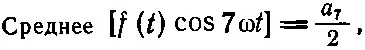 (50.8)
(50.8)
или
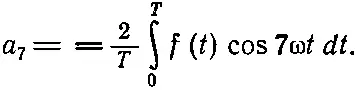 (50.9)
(50.9)
Пусть читатель сам докажет, что коэффициенты b 7, например, находятся с помощью умножения (50.2) на sin 7ω t и усреднения обеих частей. Результат таков:
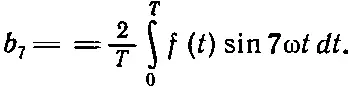 (50.10)
(50.10)
Но то, что верно для 7, очевидно, верно и для любого другого целого числа. Теперь мы запишем результат нашего доказательства в следующей, более элегантной математической форме. Если m и n — целые отличные от нуля числа и если ω=2π/T, то
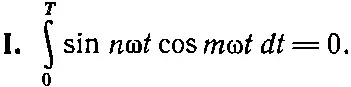 (50.11)
(50.11)
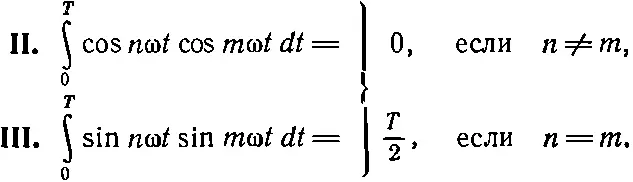 (50.12)
(50.12)
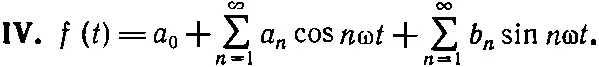 (50.13)
(50.13)
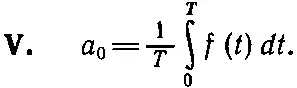 (50.14)
(50.14)
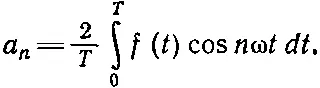 (50.15)
(50.15)
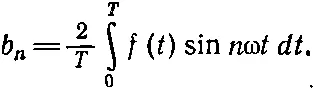 (50.16)
(50.16)
В предыдущих главах для описания простого гармонического движения было удобно пользоваться экспоненциальной функцией. Вместо cosωt мы использовали Re ехр(iωt) —действительную часть экспоненциальной функции. В этой главе мы использовали синус и косинус, потому что с ними, пожалуй, немного проще проводить доказательства. Однако наш окончательный результат, уравнение (50.13), можно записать в более компактной форме:
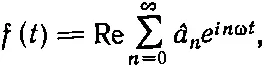 (50.17)
(50.17)
Читать дальше

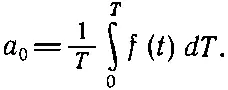 (50.3)
(50.3)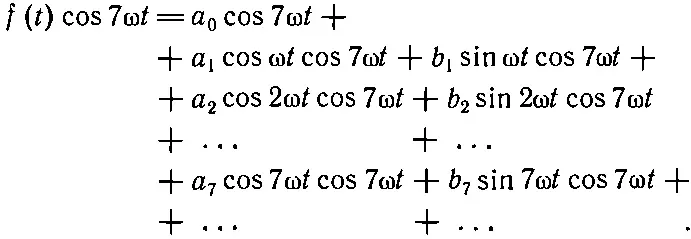 (50.4)
(50.4)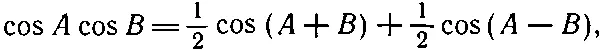 (50.5)
(50.5)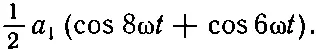 (50.6)
(50.6)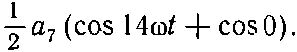 (50.7)
(50.7)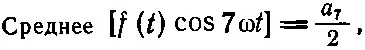 (50.8)
(50.8)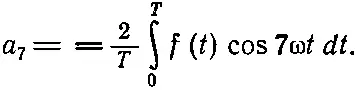 (50.9)
(50.9)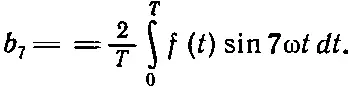 (50.10)
(50.10)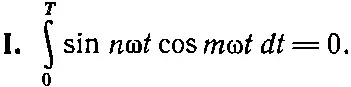 (50.11)
(50.11)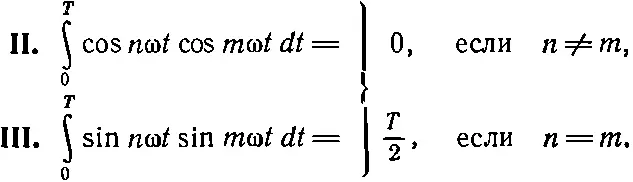 (50.12)
(50.12)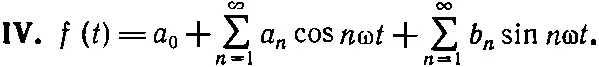 (50.13)
(50.13)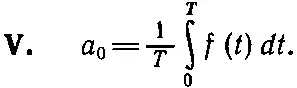 (50.14)
(50.14)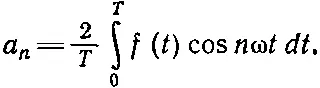 (50.15)
(50.15)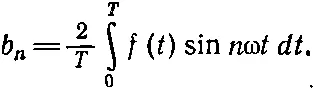 (50.16)
(50.16)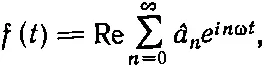 (50.17)
(50.17)




