поскольку [ f ( t )] 2=1. Таким образом мы узнали, что сумма квадратов обратных нечетных чисел равна π 2/8. Точно так же, выписав сначала ряд Фурье для функции и используя затем теорему об энергии, можно доказать результат, понадобившийся нам в гл. 45, т. е. что 1+ 1/2 4+ 1/3 4+... равно π 4/90.
Наконец, в теории гармоник есть одно очень важное явление, которое необходимо отметить, учитывая его практическую важность, но это уже относится к области нелинейных эффектов. Во всех рассмотренных нами до сих пор системах все предполагалось линейным; реакция на действие силы, например перемещение или ускорение, всегда была пропорциональна силам. Токи в электрической цепи были тоже пропорциональны напряжениям и т. д. Теперь мы хотим рассмотреть случаи, когда строгая пропорциональность отсутствует. Представим на минуту устройство, реакция которого x выход≡x выхв момент t определяется внешним воздействием x вход≡x вхв тот же момент t .
Например, x вхможет быть силой, а х вых— перемещением, или х вх — ток, а x вых— напряжение. Если бы устройство было линейное, то мы бы получили
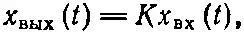 (50.24)
(50.24)
где К — постоянная, не зависящая ни от t , ни от х вх . Предположим, однако, что устройство только приблизительно линейное, т. е. на самом деле нужно писать
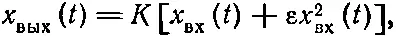 (50.25)
(50.25)
где ε мало по сравнению с единицей. Такие линейная и нелинейная реакции показаны на фиг. 50.4.
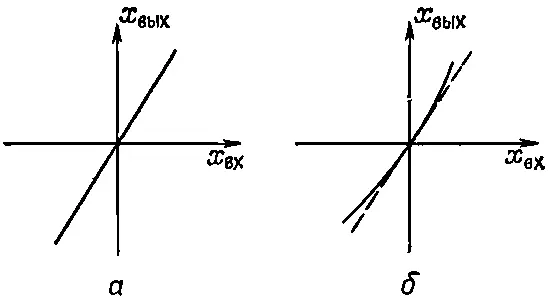
Фиг. 50.4. Реакции, а — линейная, x вых =kx вх ; б—нелинейная, x вых =k(х вх +εx 2 вх ).
Нелинейная реакция приводит к нескольким важным практическим следствиям. Некоторые из них мы сейчас обсудим. Посмотрим сначала, что получается, если пропустить через подобное устройство «чистый» тон. Пусть x вх = cos ω t . Если мы построим график зависимости x выхот времени, то получим сплошную кривую, показанную на фиг. 50.5.
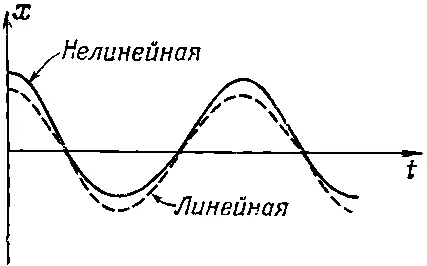
Фиг. 50.5. Реакция нелинейного устройства на входящий сигнал cosωt. Для сравнения показана линейная реакция.
Для сравнения там же проведена пунктирная кривая, представляющая реакцию линейной системы. Мы видим, что на выходе получается уже не косинусообразная функция. Она более острая в вершине и более плоская в основании. Поэтому мы говорим, что выходной сигнал искажен . Однако, как известно, такая волна не будет уже чистым тоном, а приобретает какие-то высшие гармоники. Можно найти эти гармоники. Подставляя x вх=cosωt в уравнение (50.25), получаем
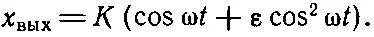 (50.26)
(50.26)
Используя равенство cos 2θ= 1/ 2(l-cos2θ), находим
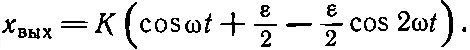 (50.27)
(50.27)
Таким образом, в выходящей волне присутствует не только основная компонента, которая была во входящей волне, но и некоторая доля второй гармоники. Кроме того, в выходящей волне появился постоянный член К (ε/2), который соответствует сдвигу среднего значения, показанному на фиг. 50.5. Эффект возникновения сдвига среднего значения называется выпрямлением . Нелинейное устройство будет выпрямлять и давать на выходе высшие гармоники. Хотя предположенная нами нелинейность только добавляет вторую гармонику, нелинейность высшего порядка, например х вх 3или x вх 4, даст уже более высокие гармоники.
Другим результатом нелинейной реакции является модуляция . Если входящая функция содержит два (или больше) чистых тона, то на выходе получатся не только их гармоники, но и другие частотные компоненты. Пусть х вх = А cosω 1t+Bcosω 2t, причем ω 1и ω 2 не находятся в рациональном отношении друг к другу. Тогда в дополнение к линейному члену (равному произведению К на входящую волну) на выходе мы получим
Читать дальше

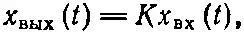 (50.24)
(50.24)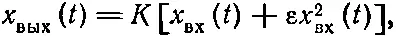 (50.25)
(50.25)

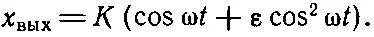 (50.26)
(50.26)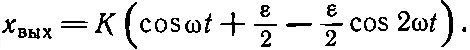 (50.27)
(50.27)




