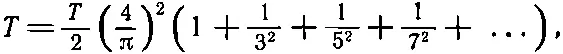где а n — комплексное число а n - ib n (с b 0=0). Если мы всюду будем пользоваться одним и тем же обозначением, то должны также написать
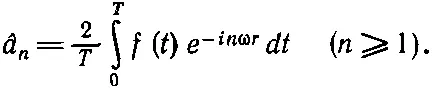 (50.18)
(50.18)
Итак, теперь мы умеем раскладывать периодическую волну на ее гармонические компоненты. Эта процедура называется разложением в ряд Фурье , а отдельные члены называются фурье - компонентами . Однако до сих пор мы не показали , что, определив все фурье-компоненты и затем сложив их, мы действительно придем назад к нашей функции f ( t ). Математики доказали, что для широкого класса функций (в сущности, для всех функций, интересных физикам), которые можно проинтегрировать, мы снова получаем f(t). Но есть одно небольшое исключение. Если функция f ( t ) разрывна, т. е. если она неожиданно прыгает от одного значения к другому, сумма Фурье такой функции даст в точке разрыва значение, лежащее посредине между верхним и нижним значениями. Таким образом, если у нас есть странная функция f ( t )=0 для 0≤ t < t 0и f ( t )=1 для t 0≤ t ≤ T , то ее сумма Фурье всюду даст нам правильную величину, за исключением точки t 0, где вместо единицы получится 1/ 2. Во всяком случае, физически даже нельзя требовать, чтобы функция была всюду нулем вплоть до точки t 0, а в самой точке t 0вдруг стала равной единице. Может быть, стоило бы специально для физиков издать такой «указ», что любая разрывная функция (которая может быть только упрощением настоящей физической функции) в точке разрыва должна принимать среднее значение. Тогда любая такая функция, с любым конечным числом «ступенек», как и все другие интересные для физики функции, будет правильно описываться рядом Фурье.
В качестве упражнения предлагаем читателю найти ряд Фурье для функции, показанной на фиг. 50.3.
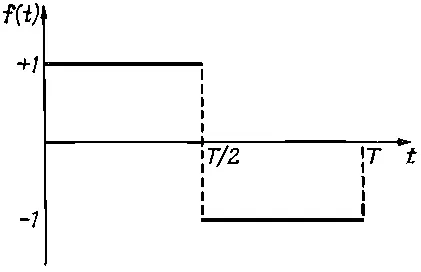
Фиг. 50.3. Ступенчатая функция. f(t)=+1 для 0
Поскольку эту функцию нельзя записать в точной алгебраической форме, то брать интеграл от 0 до Т обычным способом невозможно. Однако если разделить его на две части: по интервалу от 0 до T/2 [на котором функция f(t)=1] и по интервалу от T/2 до T [на котором f ( t ) -1], то интеграл легко берется. В результате должно получиться
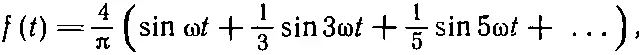 (50.19)
(50.19)
где ω=2π/T. Таким образом, оказывается, что для нашей ступенчатой волны (со специально выбранной фазой) будут только нечетные гармоники, причем их амплитуды обратно пропорциональны частотам.
Давайте проверим, что для некоторого значения t результат (50.19) действительно дает снова f ( t ). Возьмем f=T/4или ωt=π/2. Тогда
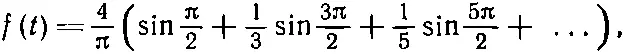 (50.20)
(50.20)
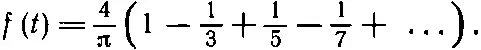 (50.21)
(50.21)
Сумма этого ряда [39]равна π/4, а, стало быть, f ( t )=1.
Энергия волны пропорциональна квадрату ее амплитуды. Для сложной волны энергия за один период пропорциональна 0∫ T f 2( t ) dt . Эту энергию можно связать с коэффициентами Фурье. Напишем
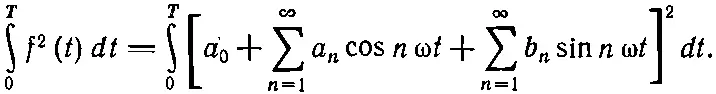 (50.22)
(50.22)
После раскрытия квадрата в правой части мы получим сумму всевозможных перекрестных членов типа a 5cos5ωtb 7cos7ωt. Однако выше мы уже показали [уравнения (50.11) и (50.12)], что интегралы от всех таких членов по одному периоду равны нулю, так что останутся только квадратные члены, подобные a 2 5 cos 25ω t . Интеграл от любого квадрата косинуса или синуса по одному периоду равен Т /2, так что получаем
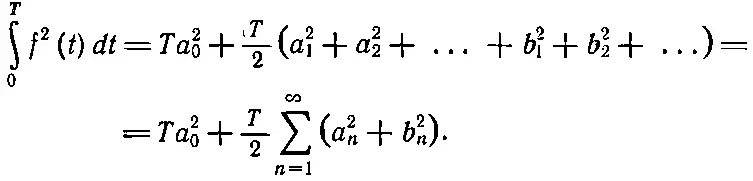 (50.23)
(50.23)
Это уравнение называют «теоремой об энергии», которая говорит, что полная энергия волны равна просто сумме энергий всех ее фурье-компонент. Применяя, например, эту теорему к ряду (50.19), мы получаем
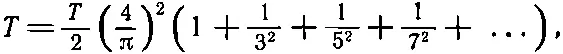
Читать дальше

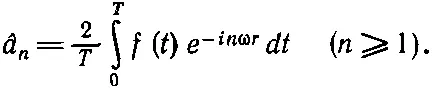 (50.18)
(50.18)
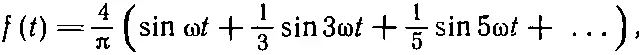 (50.19)
(50.19)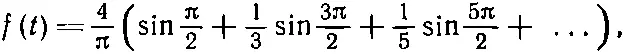 (50.20)
(50.20)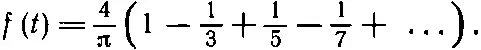 (50.21)
(50.21)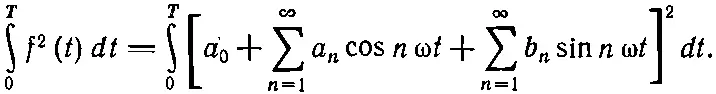 (50.22)
(50.22)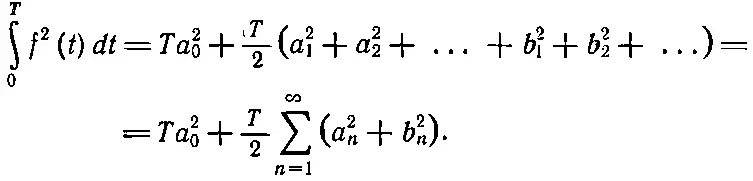 (50.23)
(50.23)