Давайте кратко рассмотрим звук, производимый вибрирующей струной.
Если оттянуть струну, а затем отпустить ее, то последующее движение будет определяться волнами, которые мы возбудили. Эти волны, как вы знаете, пойдут в обоих направлениях по струне, а затем отразятся от ее концов. Так они будут бегать взад и вперед довольно долго. И сколь бы сложны ни были эти волны, они будут повторяться периодически снова и снова.
Период этих повторений равен просто времени T, которое требуется волне, чтобы пробежать дважды всю длину струны. Ведь это как раз то время, которое необходимо для того, чтобы любая волна, отразившись от каждого конца, вернулась в начальное положение и продолжала движение в первоначальном направлении. Время, необходимое для того, чтобы волна достигла конца струны в любом направлении, одинаково. Каждая точка струны после целого периода возвращается в свое исходное положение, затем опять отклоняется от него и снова, спустя период, возвращается, и т. д.
Возникающий при этом звук тоже должен повторять те же колебания; вот почему мы, тронув струну, получаем музыкальный звук.
В предыдущей главе мы познакомились с другой точкой зрения на колеблющуюся систему. Мы видели, что в струне возникают различные собственные гармоники и что любое частное колебание, которое только возможно получить из начальных условий, можно рассматривать как составленную в надлежащей пропорции комбинацию нескольких одновременно осциллирующих собственных гармоник. Для струны мы нашли, что собственные гармоники имеют частоты ω 0, 2ω 0, 3ω 0, .... Поэтому наиболее общее движение струны складывается из синусоидальных колебаний основной частоты ω 0, затем второй гармоники 2ω 0, затем третьей гармоники Зω 0и т. д. Основная гармоника повторяется через каждый период T 1=2π/ω 0, вторая гармоника — через каждый период T 2=2π/2ω 0; она повторяется также и через каждый период Т 1=2 Т 2, т. е. после двух своих периодов. Точно таким же образом через период Т 1повторяется и третья гармоника. В этом отрезке укладываются три ее периода. И снова мы понимаем, почему задетая струна через период T 1полностью повторяет форму своего движения. Так получается музыкальный звук.
До сих пор мы говорили о движении струны. Однако звук , который представляет собой движение воздуха, вызванное движением струны, тоже должен состоять из тех же гармоник, хотя здесь мы уже не можем говорить о собственных гармониках воздуха. К тому же относительная сила различных гармоник в воздухе может быть совсем другой, чем в струне, особенно если струна «связана» с воздухом посредством «звучащей доски». Разные гармоники по-разному связаны с воздухом.
Если для музыкального тона функция f ( t ) представляет давление воздуха в зависимости от времени (скажем, такая, как на фиг. 50.1.б), то можно ожидать, что f ( t ) записывается в виде суммы некоторого числа простых гармонических функций от времени (подобных cosω t ) для каждой из различных гармонических частот. Если период колебаний равен Т , то основная угловая частота будет ω=2π/ Т , а следующие гармоники будут 2ω, 3ω и т. д.
Здесь появляется небольшое усложнение. Мы не вправе ожидать, что для каждой частоты начальные фазы обязательно будут равны друг другу. Поэтому нужно пользоваться функциями типа cos(ωt+φ). Вместо этого, однако, проще использовать для каждой частоты как синус, так и косинус. Напомним, что
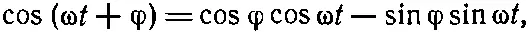 (50.1)
(50.1)
а поскольку φ — постоянная, то любые синусоидальные колебания с частотой ω могут быть записаны в виде суммы членов, в один из которых входит sinωt, а в другой — cos ω t .
Итак, мы приходим к заключению, что любая периодическая функция f ( t ) с периодом Т математически может быть записана в виде
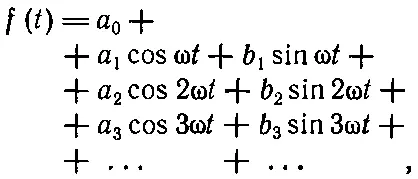 (50.2)
(50.2)
где ω=2π/T, а a и b — числовые постоянные, указывающие, с каким весом каждая компонента колебания входит в общее колебание f ( t ). Для большей общности мы добавили в нашу формулу член с нулевой частотой а 0, хотя обычно для музыкальных тонов он равен нулю. Это просто сдвиг средней величины звукового давления (т. е. сдвиг «нулевого» уровня). С этим членом наша формула верна для любого случая. Уравнение (50.2) схематически показано на фиг. 50.2.
Читать дальше

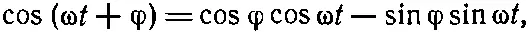 (50.1)
(50.1)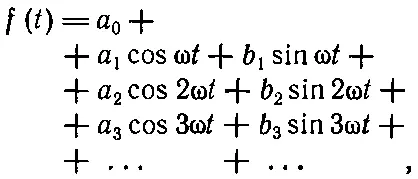 (50.2)
(50.2)




