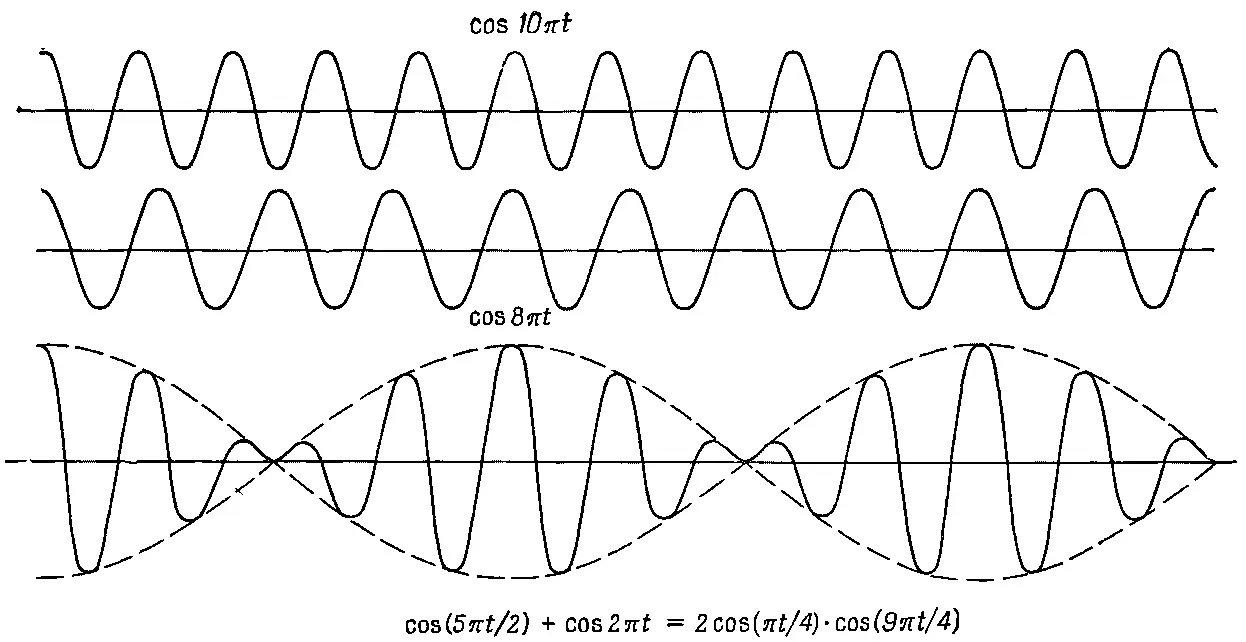
Фиг. 48.1. Суперпозиция двух косинусообразных волн с отношением частот 8:10. Точное повторение колебаний внутри каждого биения для общего случая не типично.
Математически нам нужно взять сумму двух косинусов и как-то ее перестроить. Для этого потребуются некоторые полезные соотношения между косинусами. Давайте получим их. Вы знаете, конечно, что
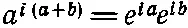 (48.1)
(48.1)
и что вещественная часть экспоненты e ia равна cosа , а мнимая часть равна sin а . Если мы возьмем вещественную часть ехр[-i( a + b )], то получим cos( a + b ), а для произведения
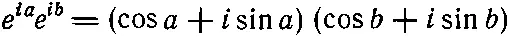
мы получаем cos a cos b -sin a sin b плюс некоторая мнимая добавка. Сейчас, однако, нам нужна только вещественная часть. Таким образом,
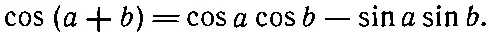 (48.2)
(48.2)
Если теперь изменить знак величины b , то, поскольку косинус при этом не изменяет знака, а синус изменяет знак на обратный, мы получаем аналогичное выражение для косинуса разности
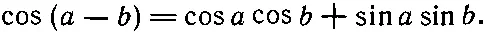 (48.3)
(48.3)
После сложения этих двух уравнений произведение синусов сократится, и мы находим, что произведение двух косинусов равно половине косинуса суммы плюс половина косинуса разности
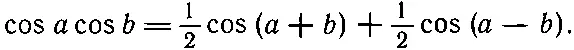 (48.4)
(48.4)
Теперь можно обернуть это выражение и получить формулу для cosα+cosβ, если просто положить α=а+b, a β=а- b , т. е. a= 1/ 2(α+β), a b= 1/ 2(α-β):
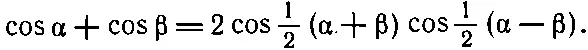 (48.5)
(48.5)
Но вернемся к нашей проблеме. Сумма cosω 1t и cosω 2t равна
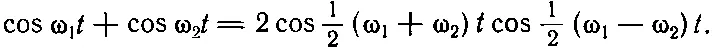 (48.6)
(48.6)
Пусть теперь частоты приблизительно одинаковы, так что 1/ 2(ω 1+ω 2) равна какой-то средней частоте, которая более или менее та же, что и каждая из них. Но разность ω 1-ω 2 гораздо меньше , чем ω 1и ω 2, поскольку мы предположили, что ω 1и ω 2приблизительно равны друг другу. Это означает, что результат сложения можно истолковать так, как будто есть косинусообразная волна с частотой, более или менее равной первоначальным, но что «размах» ее медленно меняется: он пульсирует с частотой, равной 1/ 2(ω 1-ω 2). Но та ли это частота, с которой мы слышим биения? Уравнение (48.6) говорит, что амплитуда ведет себя как cos 1/ 2(ω 1-ω 2), и это надо понимать так, что высокочастотные колебания заключены между двумя косинусоидами с противоположными знаками (пунктирная линия на фиг. 48.1). Хотя амплитуда действительно меняется с частотой 1/ 2(ω 1-ω 2), однако если речь идет об интенсивности волн, то мы должны представлять себе частоту в два раза большую. Иначе говоря, модуляция амплитуды в смысле ее интенсивности происходит с частотой ω 1-ω 2, хотя мы и умножаем на косинус половинной частоты.
Пренебрегая этими небольшими усложнениями, мы можем заключить, что если складывать две волны с частотами ω 1и ω 2, то получим волну с частотой, равной средней частоте 1/ 2(ω 1+ω 2), «сила» которой осциллирует с частотой ω 1-ω 2.
Если амплитуды двух волн различны, то можно, конечно, повторить все вычисления снова, умножив предварительно косинусы на различные амплитуды А 1и А 2и произведя массу всяких математических вычислений, перестроек и т. п. с использованием уравнений, подобных (48.2) — (48.5). Однако есть и другой, более легкий путь провести этот же анализ. Известно, например, что гораздо легче работать с экспонентами, чем с синусами и косинусами, поэтому можно представить A 1cosω 1t как реальную часть экспоненты А 1 ехр ( i ω 1 t ). Подобным же образом вторая волна будет реальной частью A 2ехр(iω 2t). После сложения этих экспонент A 1exp( i ω 1 t )+A 2exp(iω 2t) и выделения в качестве множителя экспоненты со средней частотой мы получим
Читать дальше


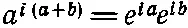 (48.1)
(48.1)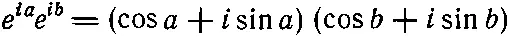
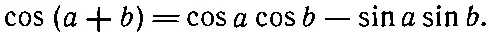 (48.2)
(48.2)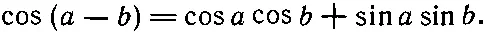 (48.3)
(48.3)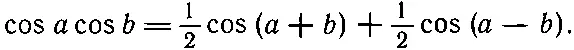 (48.4)
(48.4)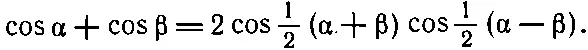 (48.5)
(48.5)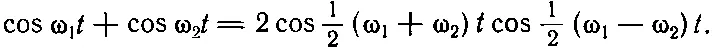 (48.6)
(48.6)




