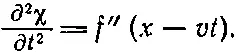 (47.15)
(47.15)
Дифференцируя эту же функцию χ по t , получаем значение — V , умноженное на производную, или ∂χ/∂ t =- vf ( x - vt ); вторая производная по времени дает
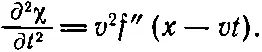 (47.16)
(47.16)
Очевидно, что f ( х - vt ) удовлетворяет волновому уравнению, если v равно c s .
Таким образом, из законов механики мы получаем, что любое звуковое возмущение распространяется со скоростью c s и, кроме того,
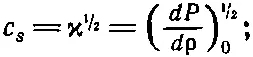
тем самым мы связали скорость звуковых волн со свойствами среды .
Легко увидеть, что звуковая волна может распространяться: и в направлении отрицательных х , т. е. звуковое возмущений вида χ( х, t )= g ( x + vt ) также удовлетворяет волновому уравнению. Единственное отличие этой волны от той, которая распространялась слева направо, заключается в знаке v , но знак д 2χ/ dt 2не зависит от выбора x + vt или х - vt , потому что в эту производную входит только v 2. Отсюда следует, что решение уравнения описывает волны, бегущие в любом направлении со скоростью c s .
Особый интерес представляет вопрос о суперпозиции решений. Допустим, мы нашли одно решение, скажем χ 1. Это значит, что вторая производная χ 1по х равна второй производной χ 1по t 1, умноженной на 1/ с s 2. И пусть есть второе решение χ 2, обладающее тем же свойством. Сложим эти два решения, тогда получается
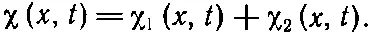 (47.17)
(47.17)
Теперь мы хотим удостовериться, что χ( х, t ) тоже представляет некую волну, т. е. χ тоже удовлетворяет волновому уравнению. Это очень просто доказать, так как
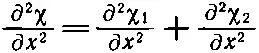 (47.18)
(47.18)
и вдобавок
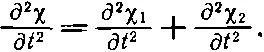 (47.19)
(47.19)
Отсюда следует, что ∂ 2χ/∂ x 2=(1/ c s 2)∂ 2χ/∂ t 2, так что справедливость принципа суперпозиции проверена. Само существование принципа суперпозиции связано с тем, что волновое уравнение линейно по χ.
Теперь естественно было бы ожидать, что плоская световая волна, распространяющаяся вдоль оси х и поляризованная так, что электрическое поле направлено по оси y, тоже удовлетворяет волновому уравнению
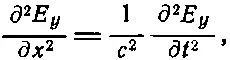 (47.20)
(47.20)
где с — скорость света. Волновое уравнение для световой волны есть одно из следствий уравнений Максвелла. Уравнения электродинамики приводят к волновому уравнению для света точно так же, как уравнения механики приводят к волновому уравнению для звука.
При выводе волнового уравнения для звука мы получили формулу , которая связывает при нормальном давлении скорость движения волны и относительное изменение давления с плотностью:
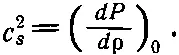 (47.21)
(47.21)
Чтобы оценить скорость изменения давления, очень важно знать, как при этом меняется температура. Можно ожидать, что в местах сгущения звуковой волны температура повысится, а в местах разрежения — понизится. Ньютон первым вычислил скорость изменения давления с плотностью, предположив, что температура при этом не меняется. Он считал, что тепло передается из одной области звуковой волны в другую так быстро, что температура измениться не успеет. Способ Ньютона дает изотермическую скорость звука, что неправильно. Правильное вычисление было сделано позже Лапласом, считавшим вопреки Ньютону, что давление и температура в звуковой волне меняются адиабатически. Поток тепла из области сгущения в область разрежения пренебрежимо мал, если только длина волны велика по сравнению с длиной свободного пробега. При этих условиях ничтожная утечка тепла в звуковой волне не влияет на скорость звука, хотя и приводит к небольшому поглощению звуковой энергии. Мы можем, естественно, ожидать, что поглощение тепла усилится, когда длина волны приблизится к длине свободного пробега, но такие длины волн примерно в миллион раз меньше длины волны слышимого звука.
Читать дальше

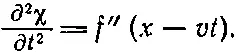 (47.15)
(47.15)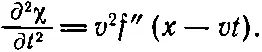 (47.16)
(47.16)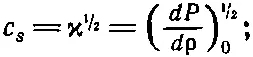
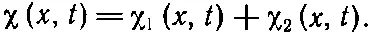 (47.17)
(47.17)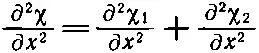 (47.18)
(47.18)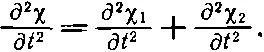 (47.19)
(47.19)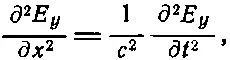 (47.20)
(47.20)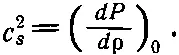 (47.21)
(47.21)




