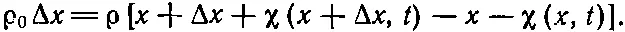 (47.5)
(47.5)
Поскольку Δx мало, можно написать χ(x+Δx, t )-χ(x,t)=(∂χ/∂ x )Δx. Здесь уже появляется частная производная, потому что χ зависит и от x, и от времени. Наше уравнение принимает вид
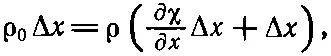 (47.6)
(47.6)
или
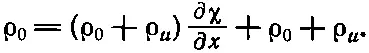 (47.7)
(47.7)
Но в звуковой волне все изменения малы, так что ρ uмало, χ мало и ∂χ/∂ x тоже мало. Поэтому в уравнении, которое мы только что написали,
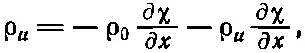 (47.8)
(47.8)
можно пренебречь ρ u (∂χ/∂ x ) по сравнению с ρ 0(∂χ/∂ x ). Так мы приходим к соотношению, которое требовалось согласно свойству I:
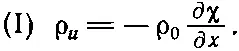 (47.9)
(47.9)
Именно такой вид уравнения можно было ожидать из чисто физических соображений. Если смещение различно для разных х , плотность будет изменяться. Знак тоже правильный: если смещение χ растет с ростом х , так что воздух расширяется, плотность должна уменьшаться.
Теперь нам нужно найти третье уравнение — уравнение движения, производимого избытком давления. Зная соотношение между силой и давлением, можно получить уравнение движения. Возьмем объем воздуха толщиной Δ x и с единичной площадью грани, перпендикулярной х , тогда масса воздуха в этом объеме есть ρ 0Δ x , а ускорение воздуха есть ∂ 2χ/∂ t 2, так что масса, умноженная на ускорение для этого слоя, есть ρ 0Δx(∂ 2χ/∂t 2). (Если Δx мало, то безразлично, где брать ускорение — на краю слоя или где-нибудь посредине.) Сила, действующая на единичную площадку нашего слоя, перпендикулярную оси x, должна быть равна ρ 0Δx(∂ 2χ/∂t 2). В точке х мы имеем силу Р ( х,t ), действующую на единицу площади в направлении + х , а в точке x+Δx возникает сила в обратном направлении, по величине равная Р(x+Δx, t ) (фиг. 47.4):
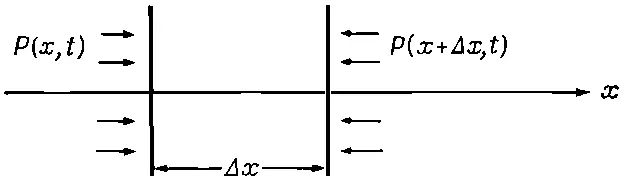
Фиг. 47.4. Результирующая сила в направлении оси х, возникающая за счет давления на единичную площадку, перпендикулярную к оси х, есть — (∂P/∂x)Δх.
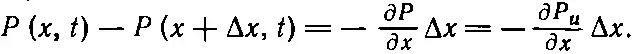 (47.10)
(47.10)
Мы учли, что Δx мало и что только избыточное давление Р u меняется в зависимости от х . Итак, согласно свойству III мы получаем
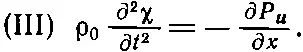 (47.11)
(47.11)
Теперь уже уравнений достаточно, чтобы увязать все величины и привести к одной переменной, скажем х . Можно выразить Р u в (47.11) с помощью (47.4):
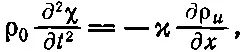 (47.12)
(47.12)
а затем исключить ρ uс помощью (I). Тогда ρ 0сократится и у нас останется
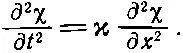 (47.13)
(47.13)
Обозначим с s 2=ϰ, тогда можно написать
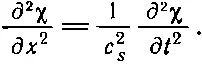 (47.14)
(47.14)
Это и есть волновое уравнение, которое описывает распространение звука в среде.
§ 4. Решения волнового уравнения
Посмотрим теперь, действительно ли волновое уравнение описывает основные свойства звуковых волн в среде. Прежде всего мы хотим вывести, что звуковое колебание, или возмущение, движется с постоянной скоростью. Кроме того, нам нужно доказать, что два различных колебания могут свободно проходить друг через друга, т. е. принцип суперпозиции. Мы хотим еще доказать, что звук может распространяться и вправо и влево. Все эти свойства должны содержаться в нашем одном уравнении.
Раньше мы отмечали, что любое возмущение, имеющее вид плоской волны и движущееся с постоянной скоростью, записывается в виде f ( x - vt ). Посмотрим теперь, является ли f ( x - vt ) решением волнового уравнения. Вычисляя ∂χ/∂ x , получаем производную функции d χ/ dx = f '( x - vt ). Дифференцируя еще раз, находим
Читать дальше

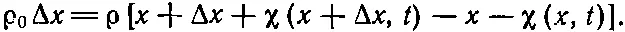 (47.5)
(47.5)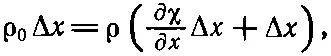 (47.6)
(47.6)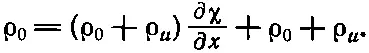 (47.7)
(47.7)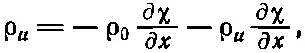 (47.8)
(47.8)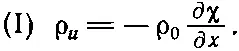 (47.9)
(47.9)
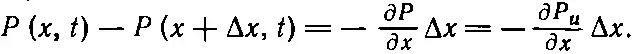 (47.10)
(47.10)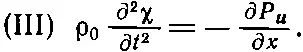 (47.11)
(47.11)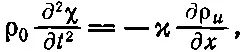 (47.12)
(47.12)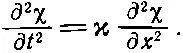 (47.13)
(47.13)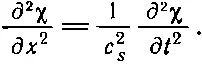 (47.14)
(47.14)




