Фиг. 41.5. Уровни энергии гармонического осциллятора. Отстоят друг от друга но равных расстояниям E n =nℏω.
Аргументы Планка выглядят немного сложнее наших, ведь это было самым началом квантовой механики, и ему приходилось кое-что доказывать. Ну, а мы просто примем как факт (который Планк и установил), что вероятность того, что занят уровень энергии Е , равна Р ( Е )=α ехр (- E / kT ). Исходя из этого, мы получим правильный результат.
Предположим, что у нас есть много осцилляторов и каждый колеблется с частотой ω 0. Некоторые из них находятся в низшем квантовом состоянии, другие забрались на уровень выше и т. д. Нам нужно знать среднюю энергию этих осцилляторов. Чтобы найти ее, давайте вычислим полную энергию всех осцилляторов и поделим результат на их число. Тогда мы получим среднюю энергию на осциллятор при тепловом равновесии, а это то же самое, что и энергия при равновесии с излучением черного тела, и ее надо подставить в уравнение (41.13) вместо kT .
Пусть N 0— число осцилляторов в основном состоянии (состоянии с наименьшей энергией), N 1— число осцилляторов в состоянии Е 1, N 2— число осцилляторов в состоянии E 2и т. д. Согласно гипотезе (которую мы не доказали), классические выражения для вероятности ехр(-п. э./kT) или ехр(-к. э ./ kT ) заменяются в квантовой механике на ехр(-Δ E / kT ), где ΔE — разность энергий. Можно утверждать, что число осцилляторов в первом состоянии N 1равно произведению числа молекул в основном состоянии N 0на ехр(-ℏω/kT). Аналогично, N 2(число молекул во втором состоянии) равно N 2= N 0exp(-2ℏω/kT). Чтобы упростить алгебру, введем х =ехр(-ℏω/ kT ). Тогда все выглядит очень просто:
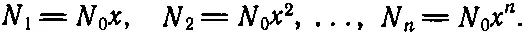
Сначала найдем полную энергию всех осцилляторов. Если осциллятор находится в основном состоянии, его энергия нуль. Если он находится в первом состоянии, то его энергия равна ℏω 0, а таких осцилляторов N 1. З начит, в этом состоянии запасена энергия N 1 ℏ ω, или ℏ ω N 0 x . Энергия осциллятора во втором состоянии 2ℏω 0, а осцилляторов N 2, поэтому мы получаем такую энергию: N 22ℏω=2ℏω 0N 0x 2и т. д. Сложив все это, найдем полную энергию E полн = N 0 ℏ ω (0+ х +2 х 2+ Зx 3+...).
А сколько всего осцилляторов? В основном состоянии, конечно, N 0, в первом состоянии N 1и т. д.; снова все сложим и получим N вcе= N 0(1+ x + x 2+ x 3+...). Поэтому средняя энергия равна
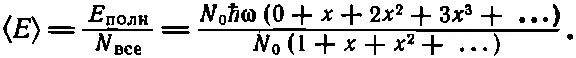 (41.14)
(41.14)
Читателям представляется возможность позабавиться этими суммами и получить от этого удовольствие. Когда вы покончите с суммированием и подставите в окончательный результат значение х , то получите, если не ошиблись
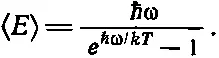 (41.15)
(41.15)
Эта формула была не только самой первой формулой, но и самой первой мыслью квантовой механики, и она явилась великолепным ответом на все недоумения предшествующих десятилетий. Максвелл уже понимал, что что-то неверно, но вопрос был в том, что же правильно ? Здесь содержится количественный ответ — что же надо взять вместо kT . Выражение для энергии, конечно, стремится к kT при ω→0 или при Т →∞. Попробуйте это доказать — здесь надо поступить так, как этому учит математика.
Выражение для средней энергии содержит знаменитый обрезающий множитель, который предвидел Джинс, и если использовать его вместо kT в (41.13), то мы получим распределение света в черном ящике:
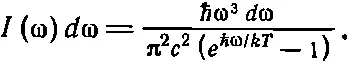 (41.16)
(41.16)
Итак, мы видим, что при больших ω кривая резко идет вниз; хотя в числителе стоит ω 3, знаменатель содержит е в чрезвычайно высокой степени; на кривой нет никакого намека на подъем, и там, где мы того не ждем, не появляется ни ультрафиолетовых, ни рентгеновских лучей!
Может возникнуть недовольство в связи с тем, что при выводе (41.16) мы пользовались квантовой теорией для уровней энергии гармонического осциллятора, а при определении эффективного сечения σ s мы оставались верны классической теории. Но квантовая теория взаимодействия света с гармоническим осциллятором приводит точно к тем же результатам, что и классическая. Это обстоятельство оправдывает то время, которое мы затратили на изучение показателя преломления и рассеяние света, основанное на представлении об атоме как о маленьком осцилляторе, — квантовые формулы получаются точно такими же.
Читать дальше

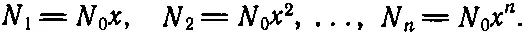
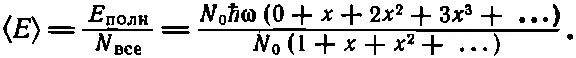 (41.14)
(41.14)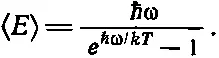 (41.15)
(41.15)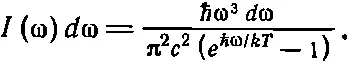 (41.16)
(41.16)




