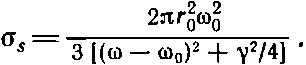 (41.9)
(41.9)
Теперь почти вся кривая загнана в область около ω=ω 0. (Фактически мы не должны делать никаких приближений, но легче иметь дело с интегралом, в котором подынтегральное выражение несколько проще.) Если умножить интенсивность в данном интервале частот на эффективное сечение рассеяния, то получится энергия, рассеянная в интервале dω. Полная рассеянная энергия — это интеграл по всем ω. Таким образом,
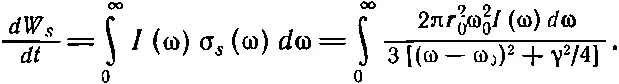 (41.10)
(41.10)
Теперь мы положим dW s / dt =3γ kT . Но почему здесь стоит 3? Потому что в гл. 32 мы предполагали, что свет поляризован так, что может раскачивать осциллятор. Если бы мы использовали осциллятор, способный раскачиваться только в одном направлении, а свет был бы, скажем, поляризован неверно, то он не рассеивался бы совсем. Поэтому мы должны либо усреднить эффективное сечение рассеяния на осцилляторе, способном раскачиваться только в одном направлении, по всем направлениям падающих пучков и поляризации света в пучке, либо, что легче сделать, представить себе, что наш осциллятор послушно следует за полем, каким бы оно ни было там, где он находится. Такой осциллятор, который одинаково легко раскачивается в любом из трех направлений, имеет среднюю энергию 3 kT , потому что у него 3 степени свободы. А раз 3 степени свободы, то надо писать 3γ kT .
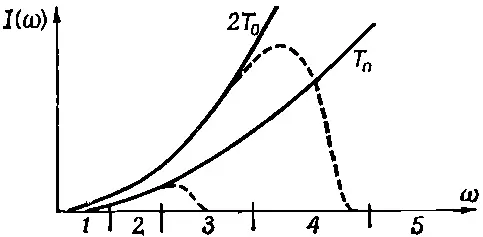
Займемся теперь интегралом. Предположим, что неизвестное спектральное распределение света I(ω) — это плавная кривая, которая в той узкой области частот, где σ sимеет острый максимум, меняется не слишком сильно (фиг. 41.3).
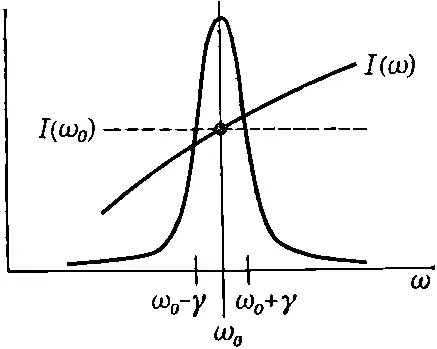
Фиг. 41.3. Сомножители подынтегрального выражения (41.10). Пик — это резонансная кривая 1/[(ω-ω 0 ) 2 +(γ 2 /4)]. Множитель I(ω) можно с хорошим приближением заменить на I(ω 0 ).
Тогда сколько-нибудь существенный вклад в интеграл дают только частоты, близкие к ω 0и отстоящие от нее на очень малую величину γ. Поэтому, хотя I(ω) неизвестная и, может быть, сложная функция, важно только ее поведение около ω=ω 0и можно заменить плавную кривую еще более ровной — «постоянной» — всюду одной высоты. Иначе говоря, мы просто вынесем I(ω) из-под знака интеграла и назовем это I(ω 0). Вынесем за интеграл и остальные постоянные и тогда получим
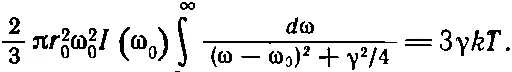 (41.11)
(41.11)
Интеграл берется от 0 до ∞, но 0 отстоит так далеко от ω 0, что кривая за это время идет почти вдоль оси абсцисс, поэтому заменим 0 на -∞, разница небольшая, а интеграл взять легче. Интеграл вида ∫ dx /( x 2+ а 2) приводит к арктангенсу. Если взглянуть в справочник, то мы увидим, что он равен π/α. Итак, для нашего случая это 2π/γ. После небольших манипуляций мы получаем
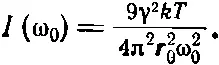 (41.12)
(41.12)
Затем мы подставим сюда формулу (41.6) для γ (мы уже не будем стараться писать ω 0; раз это верно для любой ω 0, то можно назвать ее просто ω), и формула для I(ω) примет вид
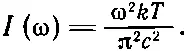 (41.13)
(41.13)
Она и определяет распределение света в горячей печке. Это так называемое излучение абсолютно черного тела . Черного потому, что, если заглянуть в топку печки при абсолютном нуле, она будет черной.
Формула (41.13) задает распределение энергии излучения внутри ящика при температуре Т согласно классической теории. Отметим сначала замечательную особенность этого выражения. Заряд осциллятора, масса осциллятора, все частные его свойства выпали из формулы; ведь если мы достигли равновесия с одним осциллятором, мы должны позаботиться о равновесии и с любым другим осциллятором другой массы, иначе будут неприятности. Таким образом, это важный способ проверки нашей теоремы о том, что равновесие зависит только от температуры , а не от того, что приводит к равновесию. Теперь можно начертить кривую I(ω) (фиг. 41.4).
Читать дальше

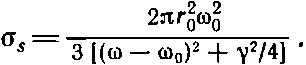 (41.9)
(41.9)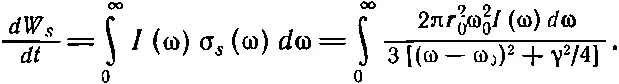 (41.10)
(41.10)
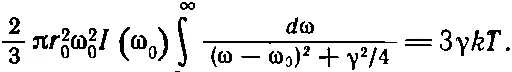 (41.11)
(41.11)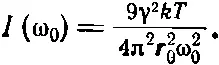 (41.12)
(41.12)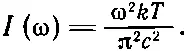 (41.13)
(41.13)





