А теперь подсчитаем, насколько должен быть освещен ящик при температуре Т , чтобы рассеяние света на осцилляторе обеспечивало его как раз такой энергией, какая нужна для поддержания излучения. Пусть атомов в ящике совсем немного и находятся они далеко друг от друга, так что наш осциллятор идеальный, не имеющий иного трения, кроме радиационного. Теперь заметим, что при тепловом равновесии осциллятор делает сразу два дела. Во-первых, он излучает, и мы можем подсчитать энергию излучения. Во-вторых, он в возмещение получает точно такое же количество энергии в результате рассеяния на нем света. Поскольку энергия ниоткуда больше притечь не может, то эффективное излучение — это как раз та часть «общего света», которая рассеялась на осцилляторе.
Таким образом, прежде всего мы вычисляем энергию, излучаемую в 1 сек осциллятором с заданной энергией. (Мы позаимствуем для этого в гл. 32, посвященной радиационному трению, несколько равенств и не будем здесь приводить их выводы.) Отношение энергии, излученной за радиан, к энергии осциллятора называется 1/ Q [см. уравнение (32.8)] : 1/ Q =( dW / dt )/ω 0 W . Используя величину γ (постоянную затухания), можно записать это в виде 1/ Q =γ/ω 0, где ω 0— собственная частота осциллятора, если γ очень мала, а Q очень велико. Излученная за 1 сек энергия равна
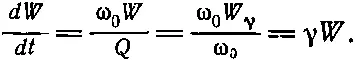 (41.4)
(41.4)
Излученная за 1 сек энергия просто равна произведению γ на энергию осциллятора. Средняя энергия нашего осциллятора равна kT , поэтому произведение γ на kT — это среднее значение излученной за 1 сек энергии:
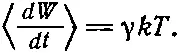 (41.5)
(41.5)
Теперь нам нужно только узнать, что такое γ. Эту величину легко найти из уравнения (32.12):
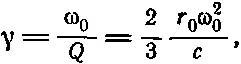 (41.6)
(41.6)
где r 0= e 2/ mc 2— классический радиус электрона, и мы положили λ=2πс/ω 0.
Окончательный результат для средней скорости излучения света вблизи частоты ω 0таков:
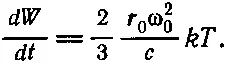 (41.7)
(41.7)
Теперь надо выяснить, сильно ли должен быть освещен осциллятор. Освещение должно быть таким, чтобы поглощенная осциллятором энергия (и впоследствии рассеянная) была в точности равна предыдущей величине. Иначе говоря, излученный свет — это свет, рассеянный при освещении осциллятором в полости. Итак, нам остается рассчитать, сколько света рассеивается осциллятором, если на него падает какая-то — неизвестная — доза излучения. Пусть I(ω)dω— энергия света частоты ω в интервале частот d ω (ведь у нас нет света точно заданной частоты; излучение распределено по спектру). Таким образом, I(ω) — это спектральное распределение , которое нам надо найти. Это тот цвет огня, который мы увидим внутри печи при температуре Т , если откроем дверцу и заглянем внутрь. Сколько же все-таки света поглотится? Мы уже определяли количество излучения, поглощаемого из заданного падающего пучка света, и выразили его через эффективное сечение . Это соответствует тому, как если бы мы предполагали, что весь свет, падающий на площадку определенной площади, поглощается. Таким образом, полная переизлученная (рассеянная) интенсивность равна произведению интенсивности падающего света I(ω)dω на эффективное сечение σ.
Мы вывели формулу для эффективного сечения [см. уравнение (31.19)], не включающую затухания. Нетрудно повторить этот вывод снова и учесть трение, которым мы тогда пренебрегли. Если это сделать, то, вычисляя эффективное сечение по прежнему образцу, мы получим
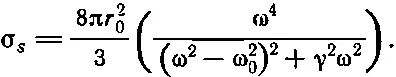 (41.8)
(41.8)
Пойдем дальше; σ s как функция частоты имеет более или менее заметную величину только для ω около собственной частоты ω 0. (Вспомним, что для излучающего осциллятора Q — порядка 10 8.) Когда ω равна ω 0, осциллятор рассеивает очень сильно, а при других значениях ω он почти не рассеивает совсем. Поэтому можно заменить ω на ω 0, а ω 2-ω 0 2на 2ω 0(ω-ω 0); тогда
Читать дальше

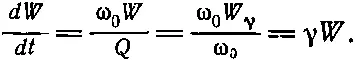 (41.4)
(41.4)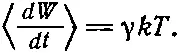 (41.5)
(41.5)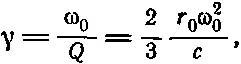 (41.6)
(41.6)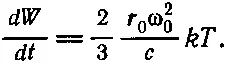 (41.7)
(41.7)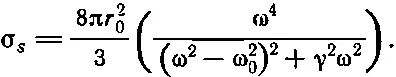 (41.8)
(41.8)




