Сопротивление механического осциллятора, конечно, пропорционально γ. В нашем случае γ — это R / L . Теперь, если увеличивать γ, то в столь приятных нам решениях (24.14) и (24.15) наступает беспорядок; когда γ/2 становится больше ω 0, решения приходится записывать по-другому:
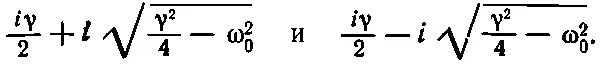
Это снова два решения, которые приводят нас к решениям exp(iα 1t) и exp(iα 2t). Подставив теперь α 1, получим
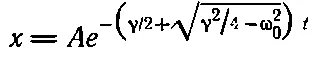
Никаких колебаний. Чисто экспоненциальное убывание. То же самое дает и второе решение
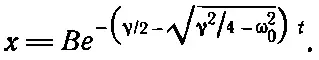
Заметим, что квадратный корень не может превысить γ/2; даже если ω 0=0, оба члена равны. Если же ω 2 0отличается от γ 2/4, то квадратный корень меньше γ/2 и выражение в круглых скобках всегда положительно. Это очень хорошо! Почему? Да потому что если бы это выражение было отрицательным, то е пришлось бы возводить в положительную степень и мы получили бы возрастающее со временем решение. Но при увеличении в цепи сопротивления колебания не могут возрастать, значит, мы избегли противоречия. Итак, мы получили два решения; оба решения экспоненциально затухают, но одно из них стремится «умереть» гораздо скорее. Общее решение, конечно, представляет собой комбинацию обоих решений, а значения коэффициентов А и В зависят от того, как начинаются колебания, каковы начальные условия. В нашей цепи случилось так, что А — отрицательное число, а В — положительное, поэтому на экране осциллоскопа мы увидели разность двух экспонент.
Давайте обсудим, как найти коэффициенты А и В (или А и A *), если известны начальные условия. Предположим, что в момент t=0 нам известны смещение х = х 0и скорость dx / dt = v 0. Если в соотношения
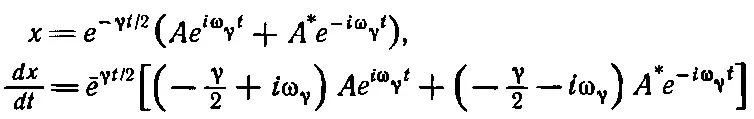
подставить значения t=0, х = х 0, dx / dt = v 0и воспользоваться тем, что е 0=е i0=1, то мы получим
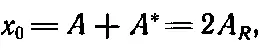
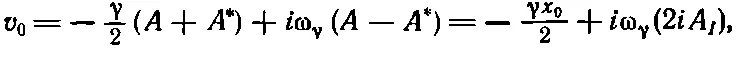
где A = A R + iA I , A *= A R — iA I . Значит,
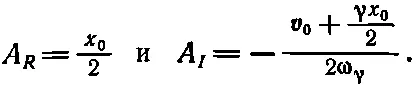 (24.21)
(24.21)
Таким образом, зная начальные условия, мы полностью определили А и А *, а значит, и кривую переходного решения. Можно записать решение и по-другому. Вспомним, что
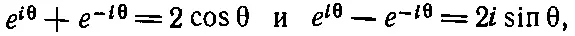
тогда
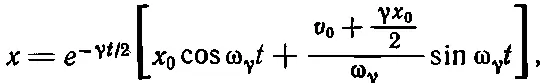 (24.22)
(24.22)
где ωγ=+√(ω 2 0-(γ 2/4). Мы получили формулу затухающих колебаний. Такая формула нам не понадобится, однако отметим ее особенности, справедливые и в более общих случаях.
Прежде всего поведение системы, на которую не действует внешняя сила, описывается суммой (суперпозицией) временных экспонент [мы записали их в виде exp(iαt)]. Такое решение хорошо передает истинное положение вещей. В общем случае α — это комплексное число, и его мнимая часть соответствует затуханию колебаний. Наконец, тесная математическая связь синусоидальных и экспоненциальных функций, о которой говорилось в гл. 22, физически часто проявляется в переходе от колебаний к чисто экспоненциальному затуханию при критических значениях некоторых параметров системы (в нашем случае это было сопротивление γ).
Глава 25 ЛИНЕЙНЫЕ СИСТЕМЫ И ОБЗОР
§ 1. Линейные дифференциальные уравнения
В этой главе мы снова вернемся к некоторым аспектам наших колебательных систем, только постараемся теперь увидеть нечто более общее, стоящее за спиной каждой частной системы. Изучение каждой колебательной системы сводилось к решению дифференциального уравнения
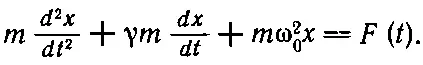 (25.1)
(25.1)
Читать дальше

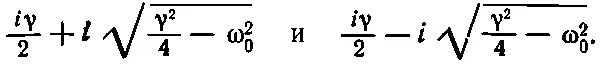
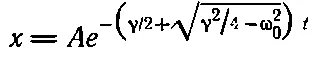
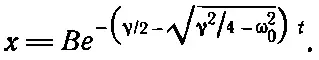
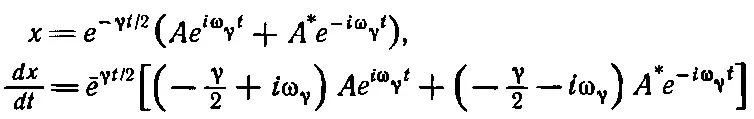
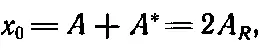
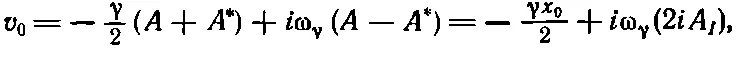
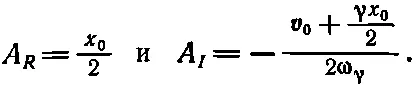 (24.21)
(24.21)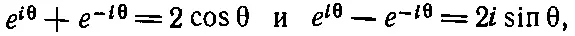
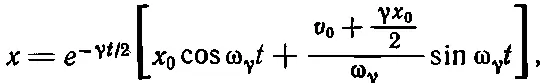 (24.22)
(24.22)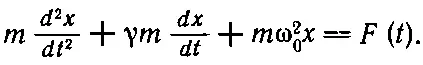 (25.1)
(25.1)




