Теперь нам известно значение энергии в любой момент. Какой будет приближенная формула, определяющая амплитуду колебаний как функцию времени? Той же самой? Нет! Потенциальная энергия пружины изменяется как квадрат смещения , кинетическая энергия — как квадрат скорости ; это приводит к тому, что полная энергия пропорциональна квадрату смещения. Таким образом, смещение (амплитуда колебаний) будет уменьшаться с половинной скоростью. Иначе говоря, мы ожидаем, что решение в случае затухающего переходного движения будет выглядеть как колебание с частотой, близкой к резонансной частоте ω 0; амплитуда этого колебания будет уменьшаться как exp(-γ t /2)
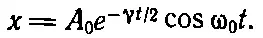 (24.10)
(24.10)
Эта формула и фиг. 24.1 дают представление о том, чего следует ожидать, а теперь приступим к точному анализу движения, т. е. к решению дифференциального уравнения движения.
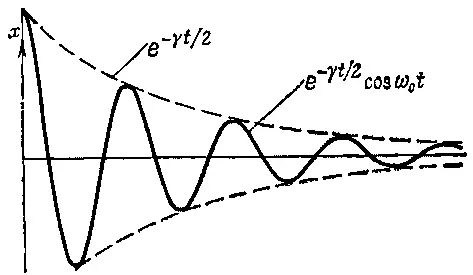
Фиг. 24.1. Затухающие колебания.
Как же решить уравнение (24.1), если выкинуть из него внешнюю силу? Будучи физиками, мы интересуемся не столько методом , сколько самим решением . Поскольку мы люди уже опытные, попытаемся представить решение в виде экспоненциальной кривой, х = А exp(iαt). (Почему мы так поступили? Оттого, что экспоненту легче всего дифференцировать!) Подставим это выражение в (24.1), помня о том, что каждое дифференцирование х по времени сводится к умножению на i α [напомним, что F ( t )=0]. Сделать это очень легко, и наше уравнение примет вид
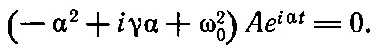 (24.11)
(24.11)
Левая часть равенства должна быть равна нулю все время , но это возможно только в двух случаях: а) А =0, однако это даже и не решение: ведь тогда все покоится, или б)
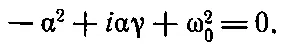 (24.12)
(24.12)
Если мы сможем решить это уравнение и найти α, то мы найдем и решение, амплитуда которого А не обязательно равна нулю!
 (24.13)
(24.13)
Чтобы не думать о том, как извлечь квадратный корень, предположим, что γ/2 меньше ω 0, и поэтому ω 0 2-γ 2/4 — положительная величина. Беспокоит другое: почему мы получили два решения! Им соответствуют
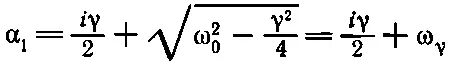 (24.14)
(24.14)
и
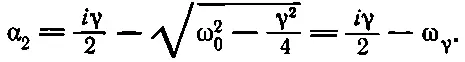 (24.15)
(24.15)
Займемся пока первым решением, предположив, что мы ничего не знаем о том, что квадратный корень принимает два значения. В этом случае смещение х равно x 1=Aexp(iα 1t), где А — произвольная постоянная. Чтобы сократить запись, введем специальное обозначение для входящего в α 1квадратного корня: √(ω 0 2-γ 2/4)=ω γ
Так, iα 1=—γ/2+ i ω γи x= A exp[—(γ/2- i ω γ)t], или, если воспользоваться замечательным свойством экспоненты,
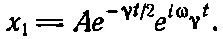 (24.16)
(24.16)
Итак, система осциллирует с частотой ω γ, которая в точности не равна частоте ω 0, но практически близка к ней, если система достаточно добротна. Кроме того, амплитуда колебаний экспоненциально затухает! Если взять действительную часть (24.16), то мы получим
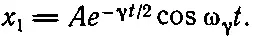 (24.17)
(24.17)
Это решение очень напоминает угаданное нами решение (24.10), вот только частота немного другая, ω γ. Но это лишь небольшая поправка, значит, первоначальная идея была правильной. И все-таки не все благополучно! А не благополучно то, что существует второе решение .
Этому решению соответствует α 2, и оно отличается от первого лишь знаком ω γ
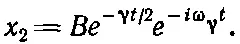 (24.18)
(24.18)
Что все это значит? Скоро мы докажем, что если x 1и х 2— возможные решения (24.1) при F ( t )=0, то х 1+х 2—тоже решение этого уравнения! Таким образом, общее решение имеет вид
Читать дальше

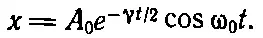 (24.10)
(24.10)
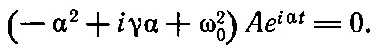 (24.11)
(24.11)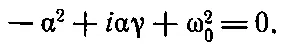 (24.12)
(24.12) (24.13)
(24.13)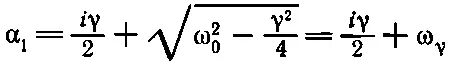 (24.14)
(24.14)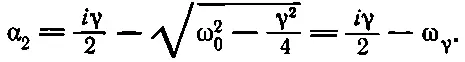 (24.15)
(24.15)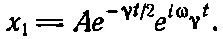 (24.16)
(24.16)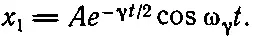 (24.17)
(24.17)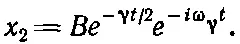 (24.18)
(24.18)




