Действительная часть квадрата комплексного числа не равна квадрату действительной части, она содержит еще и мнимую часть первоначального числа. Таким образом, если мы захотим найти энергию и посмотреть на ее превращения, нам придется на время забыть о комплексных числах.
Итак, истинно физическая величина А — это действительная часть A 0exp[i(ωt+Δ)], т. е. A = A 0соs(ωt+Δ), а комплексное число ^ А — это A 0exp(iΔ). Квадрат этой физической величины равен A 0 2cos 2(ωt+Δ). Он изменяется от нуля до максимума, как это предписывается квадратом косинуса. Максимальное значение квадрата косинуса равно 1, минимальное равно 0, а его среднее значение — это 1/ 2.
Зачастую нас совсем не интересует энергия в каждый данный момент колебания; во многих случаях достаточно знать лишь среднюю величину A 2( среднее значение квадрата А в течение времени, много большего, чем период колебаний). При этих условиях можно усреднить квадрат косинуса и доказать теорему: если А представляется комплексным числом, то среднее значение А 2равно 1/ 2 A 0 2. Здесь А 0 2— это квадрат модуля комплексного числа А . (Квадрат модуля ^ A записывают по-разному: |^ A | 2или ^ A ^ A *— в виде произведения числа ^ A на комплексно сопряженное.) Эта теорема пригодится нам еще много раз.
Итак, речь идет об энергии осциллятора, на который действует внешняя сила. Движение такого осциллятора описывается уравнением
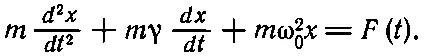 (24.1)
(24.1)
Мы, конечно, предполагаем, что F ( t ) пропорциональна cos ω t . Выясним теперь, много ли приходится этой силе работать. Работа, произведенная силой в 1 сек , т. е. мощность, равна произведению силы на скорость. [Мы знаем, что работа, совершаемая за время dt , равна Fdx , а мощность равна F ( dx / dt ).] Значит,
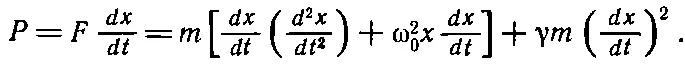 (24.2)
(24.2)
Как легко проверить простым дифференцированием, первые два члена можно переписать в виде ( d / dt )[ 1/ 2 m ( dx / dt ) 2+ 1/ 2 m ω 0 2 x 2]. Выражение в квадратных скобках — производная по времени суммы двух членов. Это понятно; ведь первый член суммы — кинетическая энергия движения, а второй — потенциальная энергия пружины. Назовем эту величину запасенной энергией , т. е. энергией, накопленной при колебаниях. Давайте усредним мощность по многим циклам, когда сила включена уже давно и осциллятор изрядно наколебался. Если пробег длится долго, запасенная энергия не изменяется; производная по времени дает эффект, в среднем равный нулю. Иными словами, если усреднить затраченную за долгое время мощность, то вся энергия поглотится из - за сопротивления, описываемого членом γ m ( dx / dt ) 2. Определенную часть энергии осциллятор, конечно, запасет, но если усреднять по многим циклам, то количество ее не будет меняться со временем. Таким образом, средняя мощность
равна
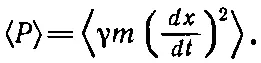 (24.3)
(24.3)
Применяя метод комплексных чисел и нашу теорему о том, что < А 2>= 1/ 2 A 0 2, легко найти эту среднюю мощность. Так как x =^ x exp( i ω t ), то dx / dt = i ω^ x exp( i ω t ). Следовательно, средняя мощность равна
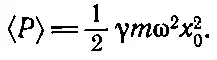 (24.4)
(24.4)
Если перейти к электрическим цепям, то dx / dt надо заменить на ток I (I — это dq / dt , где q соответствует х ), а m γ — на сопротивление R . Значит, скорость потери энергии (мощности силы) в электрической цепи равна произведению сопротивления на средний квадрат силы тока
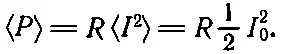 (24.5)
(24.5)
Энергия, естественно, переходит в тепло, выделяемое сопротивлением; это так называемые тепловые потери, или джоулево тепло.
Интересно разобраться также в том, много ли энергии может накопить осциллятор. Не путайте этого вопроса с вопросом о средней мощности, ибо хотя выделяемая силой мощность сначала действительно накапливается осциллятором, потом на его долю остается лишь то, что не поглотило трение. В каждый момент осциллятор обладает вполне определенной энергией, поэтому можно вычислить среднюю запасенную энергию . Мы уже вычислили среднее значение ( dx / dt ) 2, так что
Читать дальше

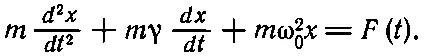 (24.1)
(24.1)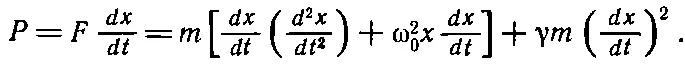 (24.2)
(24.2)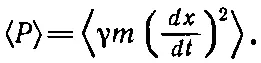 (24.3)
(24.3)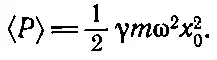 (24.4)
(24.4)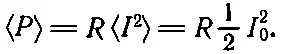 (24.5)
(24.5)




