Теоретическая идея: D. M. Greenberger, M. A. Horne, A. Shimony, A. Zeilinger, in Bell ’ s Theorem, Quantum Theory, and Conceptions of the Universe (M. Kafatos, ed.), p. 73 (Kluwer Academic, Dordrecht, 1989). Эксперимент: J. W. Pan, D. Bouwmeester, M. Daniell, H. Weinfurter and A. Zeilinger, Experimental test of quantum nonlocality in three-photon GHZ entanglement, Nature 403, 515 (2000).
Этот стандартный подход к квантовым измерениям называют копенгагенской интерпретацией в честь Нильса Бора.
Может показаться, что (2.33) эквивалентно квантовому клонированию (подразд. 2.1.3), потому что для каждого элемента базиса системы прибор эволюционирует в соответствующий элемент базиса своего гильбертова пространства. На самом деле это не так. Настоящая операция клонирования клонировала бы также и состояния суперпозиции, т. е. переводила бы правую сторону уравнения (2.33) в вид 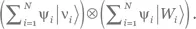 Преобразование (2.33) этого не делает и, следовательно, не противоречит теореме о запрете клонирования.
Преобразование (2.33) этого не делает и, следовательно, не противоречит теореме о запрете клонирования.
Для удобства будем предполагать, что фотон не уничтожается в ходе обнаружения, и не будем учитывать тот факт, что горизонтальные и вертикальные фотоны следуют по разным пространственным траекториям.
Эта процедура известна как мысленный эксперимент Юджина Вигнера, который поставил себя на позицию Боба, а своего гипотетического друга — на позицию Алисы.
Такой «инструментальный» подход особенно привлекал Ричарда Фейнмана, взгляды которого хорошо отражает выдуманный лозунг «Заткнись и считай» («Shut up and calculate»).
О точном виде собственного состояния импульса речь пойдет в следующей главе; пока же достаточно (2.35).
W. H. Zurek, Decoherence, einselection, and the quantum origins of the classical, Reviews of Modern Physics 75, 715 (2003).
Такие столкновения называются упругими.
E. Schrödinger, Die gegenwartige Situation in der Quantenmechanik , Naturwissenschaften 23, 807–812, 823–828, 844–849 (1935).
Состояние фотона я опустил для краткости.
Этот вывод сделан на основе статей W. H. Zurek, Environment-Assisted Invariance, Entanglement, and Probabilities in Quantum Physics, Physical Review Letters 90, 120404 (2003); Probabilities from entanglement, Born ’ s rule from invariance, Physical Review A 71, 052105 (2005).
Обратите внимание: выходное значение целевого кубита соответствует результату действия вентиля «исключающее ИЛИ» (XOR).
Теоретическая идея о квантовой телепортации впервые была опубликована в C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, W. K. Wootters, Teleporting an Unknown Quantum State via Dual Classical and Einstein — Podolsky — Rosen Channels, Physical Review Letters 70, 1895–1899 (1993). Первые эксперименты (устроенные по-разному) были проведены почти одновременно несколькими группами: D. Bouwmeester, J.-W. Pan, K. Mattle, M. Eibl, H. Weinfurter, A. Zeilinger, Experimental Quantum Teleportation, Nature 390, 6660, 575–579 (1997); D. Boschi, S. Branca, F. De Martini, L. Hardy, S. Popescu, Experimental Realization of Teleporting an Unknown Pure Quantum State via Dual classical and Einstein — Podolsky — Rosen channels, Physical Review Letters 80, 1121–1125 (1998); A. Furusawa, J. L. Sorensen, S. L. Braunstein, C. A. Fuchs, H. J. Kimble, E. S. Polzik, Unconditional quantum teleportation, Science 282, 706–709 (1998).
Теоретическая идея: M. Żukowski, A. Zeilinger, M. A. Horne, and A. K. Ekert, «Event-ready detectors»: Bell experiment via entanglement swapping, Physical Review Letters 71, 4287 (1993). Эксперимент: J.-W. Pan, D. Bouwmeester, H. Weinfurter, and A. Zeilinger, Experimental Entanglement Swapping: Entangling Photons That Never Interacted, Physical Review Letters 80, 3891 (1998).
A. I. Lvovsky, B. C. Sanders, and W. Tittel, Optical Quantum Memory, Nature Photonics 3, 706–714 (2009); N. Sangouard, C. Simon, H. De Riedmatten, and N. Gisin, Quantum repeaters based on atomic ensembles and linear optics, Reviews of Modern Physics 83, 3380 (2011).
Если вы не знакомы с дельта-функцией Дирака и преобразованием Фурье, то, прежде чем продолжить, просмотрите, пожалуйста, разделы Г.1 и Г.2 в соответствующем приложении.
Почему континуум координатных собственных состояний порождает гильбертово пространство бесконечной размерности, тогда как континуум линейно поляризованных состояний — всего лишь двумерное гильбертово пространство? Если не помните ответа, загляните в разд. 1.3.
Для более строгого рассмотрения этого вопроса вводится специальная конструкция, разработанная И. М. Гельфандом и Н. Я. Виленкиным и именуемая оснащенным гильбертовым пространством (rigged Hilbert space). Подробности в: R. de la Madrid, The role of the rigged Hilbert space in quantum mechanics, European Journal of Physics 26, 287 (2005).
На самом деле оригинальная формулировка Гейзенберга была немного иной (см. отступление 3.3).
Решение можно найти, к примеру, в: Ulf Leonhardt, Measuring the quantum state of light (Cambridge University Press, 1997).
Читать дальше
Конец ознакомительного отрывка
Купить книгу

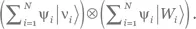 Преобразование (2.33) этого не делает и, следовательно, не противоречит теореме о запрете клонирования.
Преобразование (2.33) этого не делает и, следовательно, не противоречит теореме о запрете клонирования.








