Александр Львовский - Отличная квантовая механика

О функциях операторов см. разд. A.11.

В данном случае общая фаза в правой части уравнения (1.35) имеет значение. Дело в том, что нас интересует не только преобразование самого состояния |+⟩, но и вся линейная операция, определенная этим преобразованием. Чтобы увидеть действие этой общей фазы, вы можете попытаться решить часть a), заменив (1.35) на |+⟩ → |+⟩.

Это, конечно, фигура речи. Фотоны движутся со скоростью света, и никто не может «иметь» их на протяжении сколько-нибудь продолжительного периода времени. Утверждения о том, что у Алисы и Боба «имеется» фотон, относятся, как правило, к моменту времени непосредственно перед измерением.

Три эквивалентные части соотношения (2.1) представляют собой альтернативные варианты записи для состояний, представляющих собой тензорные произведения; мы будем считать эти варианты взаимозаменяемыми и использовать попеременно. Обратите внимание: индекс A (Алиса) или B (Боб), отмечающий принадлежность гильбертова пространства, помещается снаружи от кет-скобки. Если эти индексы опущены, то считается, что первый компонент тензорного произведения всегда относится к Алисе, а второй — к Бобу.

В первый раз эта схема была предложена и реализована в: P. G. Kwiat, E. Waks, A. G. White, I. Appelbaum, and P. H. Eberhard, Ultrabright source of polarization-entangled photons , Physical Review A 60, R773 (R) (1999).

Как правило, мы будем использовать интуитивно понятные двухиндексные обозначения для матриц состояний и операторов в составных гильбертовых пространствах. То есть каждый элемент |𝑣i⟩ ⊗ |ωj⟩ базиса тензорного произведения идентифицируется парой индексов ( i, j ), как в (2.8). Это означает, в частности, что матрица оператора имеет четыре, а не два, индекса.

W. Wootters, W. Zurek, A Single Quantum Cannot be Cloned, Nature 299, 802 (1982); D. Dieks, Communication by EPR devices, Physics Letters A 92, 271 (1982).

Порядок символов внутри бра-вектора такой же, как и внутри кет-вектора: первый символ относится к Алисе, второй — к Бобу. Индексы A и B, указывающие на конкретные гильбертовы пространства, если они есть, обычно помещаются слева от бра-векторов.

Напоминание: кубит есть любое двумерное гильбертово пространство. Примером кубита может служить поляризация фотона.

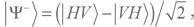Возможно, кому-то захочется ответить, что когда фотон Алисы пропадает из состояния, к примеру, то фотон Боба приобретает состояние 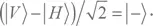Это, разумеется, неверно. Чтобы убедиться в этом, вспомните упр. 2.9, где мы выяснили, что |Ψ —⟩ можно также записать, как (|+ —⟩ — |— +⟩)/2. Это означает, что фотон Боба с равной вероятностью может находиться в состояниях |+⟩ и |—⟩.

Тот факт, что ансамбли Боба, полученные для двух измерительных базисов Алисы, идентичны, мы покажем строго в упр. 5.40.

A. Einstein, B. Podolsky, N. Rosen, Can Quantum-Mechanical Description of Physical Reality be Considered Complete? Physical Review 47, 777 (1935).

D. Bohm, Quantum Theory, Prentice-Hall, Englewood Cliffs, 1951.

Фок В. А., Эйнштейн А., Подольский Б. и др. Можно ли считать, что квантово-механическое описание физической реальности является полным? // Успехи физических наук. Т. XVI. Вып. 4 (1936). С. 440. — Прим. ред.

Там же. С. 446. — Прим. ред.

J. S. Bell, On the Einstein — Poldolsky — Rosen paradox, Physics 1, 195 (1964).

S. J. Freedman and J. F. Clauser, Experimental test of local hidden-variable theories , Physical Review Letters 28, 938 (1972).

A. Aspect, P. Grangier, G. Roger, Experimental Realization of Einstein — Podolsky — Rosen — Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities , Physical Review Letters 49, 91 (1982).

G. Weihs, T. Jennewein, C. Simon, H. Weinfurter, A. Zeilinger, Violation of Bell’s inequality under strict Einstein locality conditions , Physical Review Letters 81, 5039 (1998).

M. A. Rowe, D. Kielpinski, V. Meyer, C. A. Sackett, W. M. Itano, C. Monroe, D. J. Wineland, Experimental violation of a Bell’s inequality with efficient detection , Nature 409, 791 (2001).

B. Hensen et al ., Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres , Nature 526, 682 (2015).

M. Guistina et al. Significant-loophole-free test of Bell’s theorem with entangled photons , Physical Review Letters 115, 250401 (2015).

L. K. Shalm et al. A strong loophole-free test of local realism , Physical Review Letters 115, 250402 (2015).

Конечно, можно настроить электронику таким образом, что при отсутствии сигнала в обоих детекторах экран случайным образом покажет величину ±1. При такой программе эксперимент будет соответствовать рис. 2.2, но проблему это не решит (см. упр. 2.52).