Julian Barbour - The End of Time - The Next Revolution in Physics

Bell’s question perfectly reflects Einstein’s ‘robust realism’ – that the two-particle system ought to consist of two separate entities that possess definite properties before any measurements are made. Assuming this, Bell proceeded to derive certain inequalities, justly famous, that impose upper limits on the degree of the correlations that such ‘classical’ entities could exhibit (tighter correlations would simply be a logical impossibility). He also showed that quantum mechanics can violate these inequalities: the quantum world can be more tightly correlated than any conceivable ‘classical world’. Aspect’s experiments specifically tested the Bell inequalities and triumphantly confirmed the quantum predictions. The only way in which the atomized world after which Einstein hankered can be saved is by a physical interaction that has so far completely escaped detection and is, moreover, propagated faster than light. Einstein could hardly have taken comfort from this straw. Far better, it seems to me, is to seek understanding of the Here in Mach’s All. I shall give some indication of what I mean by this after we have considered the next topic.

In 1957, Hugh Everett, a student of John Wheeler at Princeton, proposed a novel interpretation of quantum mechanics. Its implications are startling, but for over a decade it attracted little interest until Bryce DeWitt drew wide attention to it, especially by his coinage many worlds to describe the main idea. Everett had used the sober title ‘Relative state formulation of quantum mechanics’. One well-known physicist was prompted to call it the ‘best-kept secret in physics’. So far as I know, Everett published no other scientific paper. He was already working for the Weapons Systems Evaluation Group at the Pentagon when his paper was published. He was apparently a chain smoker, and died in his early fifties.

Everett noted that in quantum mechanics ‘there are two fundamentally different ways in which the state function can change’: through continuous causal evolution and through the notorious collapse at a measurement. He aimed to eliminate this dichotomy, and show that the very phenomenon that collapse had been introduced to explain – our invariable observation of only one of many different possibilities that quantum mechanics seems to allow – is actually predicted by pure wave mechanics. Collapse is redundant.

The basis of Everett’s interpretation is the endemic phenomenon of entanglement. By its very nature, entanglement can arise only in composite systems – those that consist of two or more parts. In fact, an essential element of the many-worlds interpretation as it is now almost universally understood is that the universe can and must be divided into at least two parts – an observing part and an observed part. However, Everett himself looked forward to the application of his ideas in the context of unified field theories, ‘where there is no question of ever isolating observers and object systems. They are all represented in a single structure, the field.’ That is ultimately the kind of situation that we must consider, but for the moment we shall look at the familiar form of the interpretation.

The simplest two-particle system can be used to explain a quantum measurement. The core idea is all that counts. One particle, called the pointer , is used to establish the location of the other particle, called the object . Figure 43 shows things with which we are already familiar. At an initial time t set-up, the pointer (horizontal axis) and object (vertical axis) are not entangled. For any of the small range of possible pointer positions, the object has identical ranges of possible positions, shown schematically by points 1 to 6 on the left. Determination of the pointer position in this state would tell us nothing about the object. But the interactions of the particles are so arranged that by the later time t measurementthe wave function, passing through the interaction region, has ‘swung round’ into the position shown on the right. Remembering how points in Q translate into positions in space, we see that the object still has its original range of positions 1 to 6, but that the new pointer positions are strongly correlated with them.

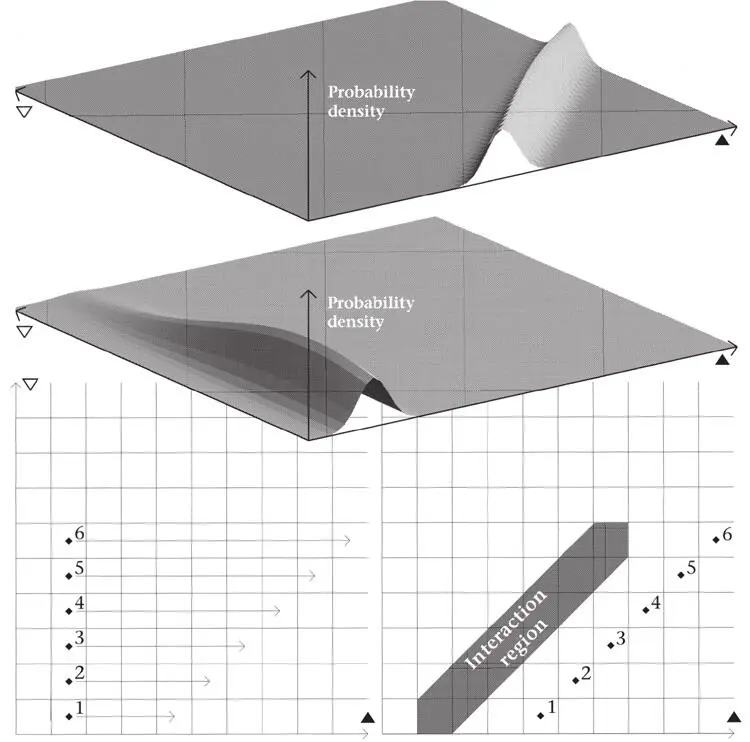
Figure 43.The initially unentangled state at t set-up, shown schematically at the bottom left by the vertical column of positions 1, 2, 3, 4, 5, 6, and the first probability density above it, evolves into the entangled state at t measurement, indicated on the right by the inclined numbers 1, 2, 3, 4, 5, 6 and the upper right probability density.

If we operate detectors at t measurementto find the pointer’s position (by letting it strike an emulsion or even, in principle, by acting ourselves as observers and placing our eyes at the appropriate places), the standard quantum rules immediately tell us the object’s position, for different pointer positions are now correlated with different object positions. Quantum measurement consists of two stages: the creation from an unentangled state of a strongly entangled state (creating the conditions of a so-called good measurement ) followed by the exploitation of the correlations in that state (using the determination of the pointer position to deduce – measure – the object’s position). The existence of such correlations has now been wonderfully well confirmed by experiments. If detectors have been used to find the pointer and are then used to locate the object directly, the quantum correlations predicted are invariably confirmed. Measurement theory is really verification of the correlations associated with entanglement. Personally, I think that the term ‘measurement’ has generated misunderstanding, and that it would be better simply to speak of verification of correlations.

The measurement problem of quantum mechanics is this: how does the entangled state of many possibilities collapse down to just one, and when does it happen? Is it when the pointer strikes the emulsion, or when the human observer sees a mark on the emulsion? I won’t go into all the complications, which depend on how much of the world we wish to describe quantum mechanically. It leads to a vicious infinite regress. You can go on asking quantum mechanics again and again to say when collapse occurs, but it never gives an answer. The different possibilities already represented at t set-upin the different positions of the object system can never be eradicated, and simply ‘infect’ the rest of the world – first the pointer, then the emulsion, then the retina of the experimentalist’s eye, finally his or her conscious state. All that the Copenhagen interpretation can say is that collapse occurs at the latest in the perceptions of the experimentalist. When it happens no one can say – it can only be said that if collapse does not happen we cannot explain the observed phenomena.

But must it happen? Everett came up with a simple – with hindsight obvious – alternative. Collapse does not happen at all: the multiple possibilities represented in the entangled state continue to coexist. In each possibility the observer, in different incarnations, sees something different, but what is seen is definite in each case. Each incarnation of the observer sees one of the possible outcomes that the Copenhagen interpretation assumes is created by collapse. The implications of this are startling. A single atomic particle – the object particle in Figure 43 – can, by becoming entangled with first the pointer and then the emulsion, and finally the conscious observer, split that observer (indeed the universe) into many different incarnations. In his paper in 1970 that at last brought Everett’s idea to wide notice, Bryce DeWitt wrote: