Julian Barbour - The End of Time - The Next Revolution in Physics

The most important thing about Schrödinger’s wave mechanics is that it is formulated not in space and time, but in a suitably chosen Q and time. This is not apparent for a single particle, for which the configuration space is ordinary space. Since most accounts of quantum mechanics consider only the behaviour of a single particle, many people are unaware that the wave function is defined on configuration space. That is where ψ lives. It makes a huge difference.

An illustration using a plastic ball-and-strut model of molecules may help to bring this home. Imagine that you are holding such a model in some definite position in a room, which can represent absolute space. There are three digital displays – I shall call them ψ meters – that show red, green and blue numbers on the wall. These numbers give the intensities of the three ‘mists’ represented by ψ for the system at the time considered. Suppose you take just one ball, representing one particle of the system, and detach it from the model. Keeping all the other balls fixed, you can move the one ball around and, courtesy of the ψ meters, see how ψ changes. As you move in each direction in space, each ψ value will change. For each point of space you can find the value of ψ. The blue ψ meter will always tell you the positions for which the probability is high or low. Suppose you do this and then return the ball to its original place.

Now move a second ball to a slightly different position, and leave it there. The ψ meters will change to new values. Once again, explore space with the first ball, watching the ψ meters. The values of ψ will be (in general) quite different. The ψ values on the displays embody information. The amount is staggering. For every single position in space to which you move any one of the other balls, you get a complete new set of values in space for the ball chosen as the ‘explorer’. And any ball can be the explorer. Each explorer will have its own distinctive three-dimensional patterns of ψ for every conceivable set of positions of the others.

Now, what is a molecule? When Richard Dawkins described the haemoglobin molecule and its six thousand million million million perfect copies in our body, he said that in its intricate thornbush structure there is ‘not a twig nor a twist out of place’. That is in a molecule containing perhaps twenty thousand atoms. But molecules are even more remarkable than that. The twig and the twist are averaged structures corresponding to the most probable configuration in which the molecule will be found. In the Schrödinger picture, the molecule is not just one structure but a huge collection of potentially present structures, each with its own probability.

In fact, the complete structure of complicated protein molecules like haemoglobin cannot be understood solely on the basis of wave mechanics. This is because of the way they are put together from amino acid units. But for simpler molecules, which may still contain many particles, you could (in imagination at least) do what I have just described for the ball-and-strut model. Start with one of the model configurations shown in chemistry textbooks, and look at the ψ meters, especially the blue one. It will give a high reading. Around that highly probable structure are other similar structures, all with a high – but not quite so high – blue intensity. Individual units of the structure – simpler forms of Dawkins’s ‘twigs’ – could be moved as a whole, say by twisting them, from the most probable configuration, and the blue intensity would drop. It would also drop if one atom of the few dozen within the twig were moved from the most-favoured position. The molecule is not just the most probable configuration. It is all possible configurations with their ψ values, held in balance by the laws of wave mechanics. The existence and most-favoured shape of molecules can be understood in no other way.

Contrary to the impression given in many books, quantum mechanics is not about particles in space: it is about systems being in configurations – at ‘points’ in a Q, or ‘hybrid Platonia’. That is something quite different from individual probabilities for individual particles being at different points of ordinary space. Each ‘point’ is a whole configuration – a ‘universe’. The arena formed by the ‘points’ is unimaginably large. And classical physics puts the system at just one point in the arena. The wave function, in contrast, is in principle everywhere.

This is what I mean by saying that Schrödinger opened the door onto a vast new arena. Compared with Schrödinger’s vistas, grander than any Wagnerian entrance into Valhalla, the Heisenberg uncertainty relation for a single particle captures little of quantum mechanics. All revolutions in physics pale into insignificance beside Schrödinger’s step into the configuration space Q. Not that he did it happily.

It is not possible to observe the extraordinary quantum arena directly. Some people do not believe it exists at all. To a large degree it has been deduced, or surmised, from phenomena observed in systems of a few particles. Getting clear, direct evidence for the quantum behaviour of single particles was difficult. It was long after Dirac made his memorable remark about each photon interfering with itself that the development of sources which release individual particles with long time intervals between releases confirmed the build-up of interference patterns in individual ‘hits’. In the last two decades, it has become possible to create in the laboratory pure quantum states of two particles, whose Q therefore has six dimensions. The quantum predictions, all verified, are not easy to explain in many words, let alone a few, and a serious attempt to do so would take me too far from my main story. The simplest possible illustration is given by two particles moving on a single line; each has a one-dimensional Q and together they have a two-dimensional configuration space (Figure 39).

As for a single particle, the maximally informative description of a quantum system at any instant t is specified by a complex wave function ψ which, in principle, has a different value at each point of the configuration space. As t changes, ψ changes. All information that can be known about the system at t is encoded in ψ at f, and consists of predictions that can be made about it. Many different kinds of prediction can be made, but they are often mutually exclusive. In a very essential way, the predictions refer to the system, not its parts.

Let us start with position predictions. Just as we did for a single particle, we can form from ψ the sum of the squares of its intensities, finding the intensity of the ‘blue mist’ (Figure 40). This gives the relative probability that the system will be found at the corresponding point in Q if an appropriate measurement is made. The important thing is that a single point in Q corresponds to positions of both particles. Anyone who has not understood this has not understood quantum mechanics. It is this fact, coupled with complementarity, that leads to the most startling quantum phenomena.

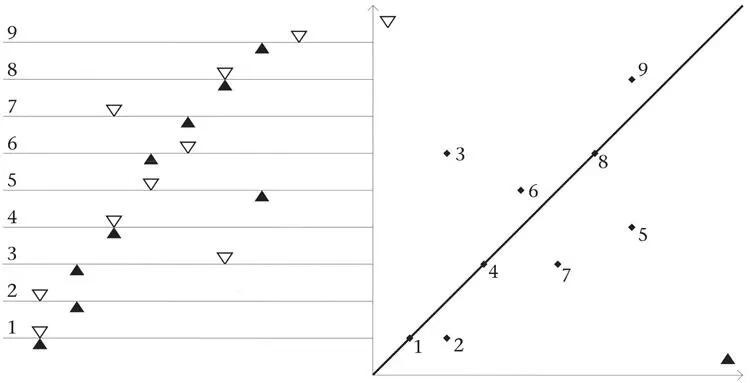
Figure 39.The two-dimensional configuration space Q of two particles on one line. The line is shown in multiple copies on the left. Nine different configurations of the two particles on it are shown. The positions of particles 1 and 2 are indicated by the black and white triangles, respectively. The axes of Q on the right show the distances of particle 1 (horizontal axis) and particle 2 (vertical axis) from the left-hand end of the line. The points on the 45° diagonal in Q correspond to configurations for which the two particles coincide (points 1, 4 and 8). You might like to check how the nine configurations on the left are represented by the nine corresponding points on the right.