Julian Barbour - The End of Time - The Next Revolution in Physics

Figure 36.The wave function of a particle with a definite momentum.

The striking thing about this situation is that the probability for the position of the particle, given by the sum of the squares of the red and green intensities, is completely uniform in space. The reason is that for two sinusoidal waves displaced by a quarter of a wavelength, this sum is always 1 if the wave’s amplitude (its height at the peaks) is 1. This is a consequence of the well-known trigonometric relation sin 2 A + cos 2 A = 1, which itself is just another expression of Pythagoras’ theorem. Thus, for a particle in this state, we have absolutely no information about its position, but we do know that it has a definite momentum.

So far we have considered waves of only one wavelength. However, we can add waves of different wavelengths. Whenever waves are added, they interfere, enhancing each other here and cancelling out there. By playing around with waves of different wavelengths we can make a huge variety of patterns (Figure 37 is an example). In fact the French mathematician Joseph Fourier (one of Napoleon’s generals) showed that more or less any pattern can be made by adding, or superposing , sinusoidal waves appropriately. Any wave pattern created in this way and concentrated in a relatively small ‘cloud’ is called a wave packet . The same pattern can be made by superpositions of quite different kinds. The primary meaning of ψ is that its value at x determines, through the squares of its two intensities, the probability that the particle will be ‘found’ at x . Now, a ‘cloud’ could be so narrow that it becomes a ‘spike’ at some value of x . The particle can then be at only one place – at the spike. Such a wave function is called a position eigenstate.

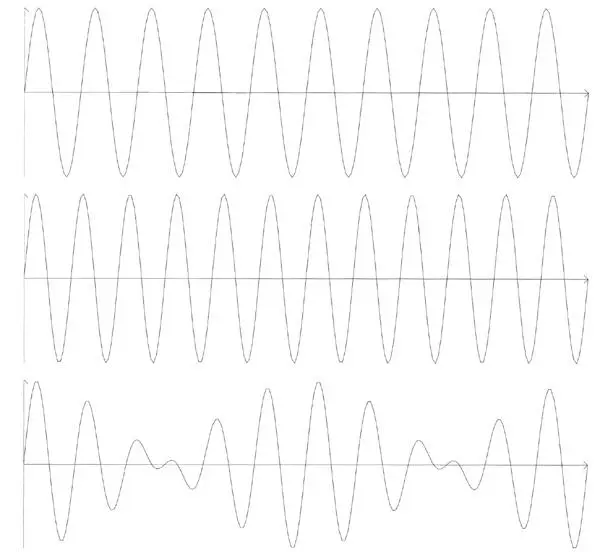
Figure 37.Superposition of the two waves at the top gives rise to the very different wave pattern at the bottom.

Thus, the same wave pattern can be regarded either as a superposition of plane waves or as a superposition of many such spikes added together with different coefficients (Figure 38). Any wave function is a superposition of either position or momentum eigenstates. There is a duality at the heart of the mathematics. What is remarkable – and constitutes the essential core of quantum mechanics in the standard form it was given by Dirac – is that it perfectly reflects a similar duality found in nature. This is where the measurement problem becomes even more puzzling. We need to consider the ‘official line’, known as the Copenhagen interpretation because it was established by Heisenberg and Bohr at the latter’s institute in Copenhagen shortly after the creation of quantum mechanics.

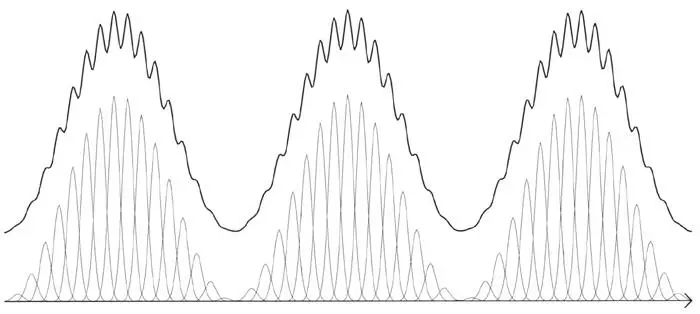
Figure 38.Two ‘spiky’ wave patterns (thin curves) are superposed to make a much smoother pattern (heavy curve).

The wave function of a particle is assumed to be a maximal representation of its physical state. It codes everything that can ever be deduced about the particle at an instant. Using it, we can predict the outcomes of experiments performed on the particle. There are two cardinal facts about these predictions. First, they are probabilistic. Only if, for example, the particle is in a momentum eigenstate (represented by the two special plane waves described above) will measurement of the momentum confirm that the particle has the corresponding momentum. If it is in a superposition of momentum eigenstates, then any one of the momenta in the superposition may be found as a result of the measurement. The probabilities for them are determined by the strengths with which the corresponding momentum eigenstates are represented in the superposition.

It is a basic Copenhagen tenet that the probabilistic statements reflect a fundamental property of nature, not simply our ignorance. It is not that before the measurement the particle does have a definite momentum and we simply do not know it. Instead, all momenta in the superposition are present as potentialities, and measurement forces one of them to be actualized. This is justified by a simple and persuasive fact. If we do not perform measurement but instead allow ψ to evolve, and only later make some measurement, then the things observed later (like the two-slit fringes) are impossible to explain unless all states were present initially and throughout the subsequent evolution. Outcomes in quantum mechanics are determined by chance at the most fundamental level. This is the scenario of the dice-playing God that so disturbed Einstein.

If anything, the second cardinal fact disturbed him even more. There seems to be a thoroughgoing indefiniteness of nature even more radical than the probabilistic uncertainties. As we have seen, one and the same state can be regarded as a superposition of either momentum or position eigenstates. It is the way this mathematics translates into physics that is startling. The experimentalist has complete freedom to choose what is to be measured: position or momentum. Both are present simultaneously as potentialities in the wave function. The experimentalist merely has to choose between set-ups designed to measure position or momentum. Once the choice is made, outcomes can then be predicted – and one outcome is actualized when the measurement is made. In fact, the indefiniteness is even greater since other quantities, or observables as they are called, such as energy and angular momentum, are also present as potentialities in ψ.

Only one experiment can be made – for position or momentum, say, but not both. Every measurement ‘collapses’ the wave function. After the collapse, the wave function, which could have been used to predict outcomes of alternative measurements, has been changed irrevocably: there is no going back to the experiment we opted not to perform. It is a very singular business. Whatever observable we decide to measure, we get a definite result. But the observable that is made definite depends on our whim. The many people who, like Einstein, believe in a real and definite world find this immensely disconcerting. What is out there in the world seems to depend on mere thoughts that come into our mind. Most commentators believe that this radical indefiniteness – the possibility to actualize either position or momentum but not both – is the most characteristic difference between classical and quantum physics. In classical physics, position and momentum are equally real, and they are also perfectly definite.

The fact that in quantum mechanics one can choose to measure one but not both of two quantities was called complementarity by Bohr. Pairs of quantities for which it holds are said to be complementary.

Heisenberg’s famous uncertainty relation gives quantitative expression to complementarity for position and momentum. De Broglie’s relation λ=h/mv=h/p determines the wavelength of a particle of momentum p=mv , where m is its mass and v its velocity. Now, it follows from Fourier’s work on the superposing of waves that a wave packet restricted to a small spatial region contains many waves in a broad spread of wavelengths. To narrow down the spatial positions q , it is necessary to broaden the range of momenta p . Conversely, to get a nearly definite p , we must accept a wide range of positions q .