Julian Barbour - The End of Time - The Next Revolution in Physics

Now it is time to talk about the ideas that Schrödinger introduced in the winter of 1925/6. That was when the door was opened onto the vast arena.

(p. 191) On the connection between particles and fields, let me mention here that I assume the appropriate ‘Platonic’ representation at the level of quantum field theory to be in terms of the states of fields, not particles.

Most accounts of quantum mechanics concentrate on the simplest situations – the behaviour of a single particle. That is already very surprising. But the really mysterious properties come to light only in composite systems of several particles, whose behaviour can become bafflingly correlated. The situation is currently very exciting because experimentalists are now able to study two widely separated but strongly correlated particles. Their observations confirm quantum mechanics brilliantly but stretch human intuition to the limit. How can such things happen in space and time? And what unbelievable scenarios will a quantum universe present?

I suspect that the present astonishment exists because most quantum theoreticians do not think enough about quantum cosmology. The first issue is its arena. Quantum mechanics is currently presented in a hybrid framework of two arenas at once. One is an abstract mathematical construct known as Hilbert space, but its elements are essentially defined by absolute space and time, which comprise the second arena. Quantum mechanics takes both for granted. But they provide only a dubious foundation for quantum cosmology. Clarity cannot be achieved until this hybrid state is ended: the space-time framework must go. The answer to the question of how such things can happen in space and time is that they do not. They neither happen nor are they to be found in space and time. But these things are, and their being is in Platonia, which must replace the Hilbert space erected on the shaky foundations of absolute space and time. That, at least, is my view.

My account of wave mechanics will aim to show that the demise of space and time is inevitable. We shall first see how a single particle is described in space and time, and then see what happens when we try to describe the universe. Space and time ‘evaporate’, and we are left with the one true arena – timeless Platonia. In this arena, quantum mechanics seems to me to take on a totally transparent form. Whether we can believe in it is another matter.

Every account of quantum mechanics includes the famous two-slit experiment, and mine is no exception (Box 11). Differences come later. The two-slit experiment is to quantum mechanics what the Michelson-Morley experiment is to relativity. The facts are simple, and show that a radical change is unavoidable. The great beauty is that the bare experimental facts directly suggest the need for and the basic form of wave mechanics.

BOX 11 The Two-Slit Experiment

If a beam of photons or electrons, all with the same energy, encounters a slit in a barrier and then impinges on a screen behind it, individual localized ‘hits’ invariably occur (Figure 32). This is so even if the beam has a very low density, so that at most one particle at a time is passing through the system. This strongly suggests that individual particles leave the beam generator, pass through the slit, and strike the screen. The impacts have a characteristic distribution over a region.

Now introduce a second identical slit in the barrier (Figure 33). The interpretation of the first experiment in terms of individual particles yields an unambiguous prediction for what will happen. The argument is as follows. All particles travel towards the barrier at right angles to it, and can be assumed to be uniformly distributed in space. The pattern behind a single slit is presumably created by the interaction between the particles and the slit as they pass through it. Entering the slit at different positions, the particles will have different deflections and will thus strike the screen at different points. When two slits are open, each should have an effect identical to that of the single slit, so the combined pattern should be simply the sum of the effects of two single slits.

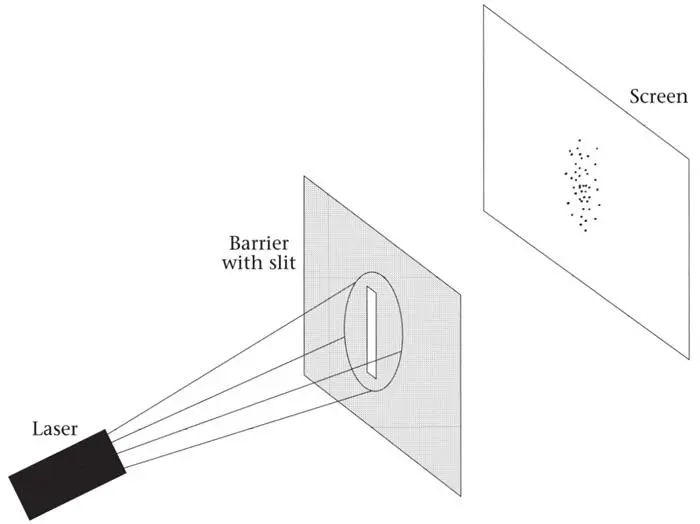
Figure 32.The distribution of hits behind one slit.

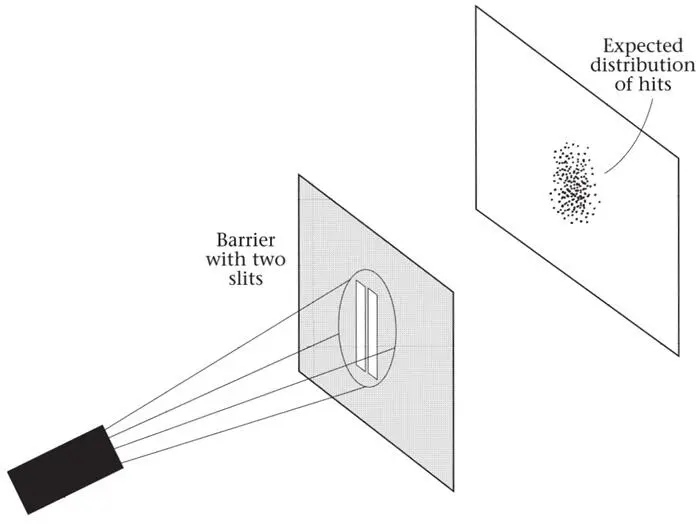
Figure 33.The expected distribution of hits behind two slits.

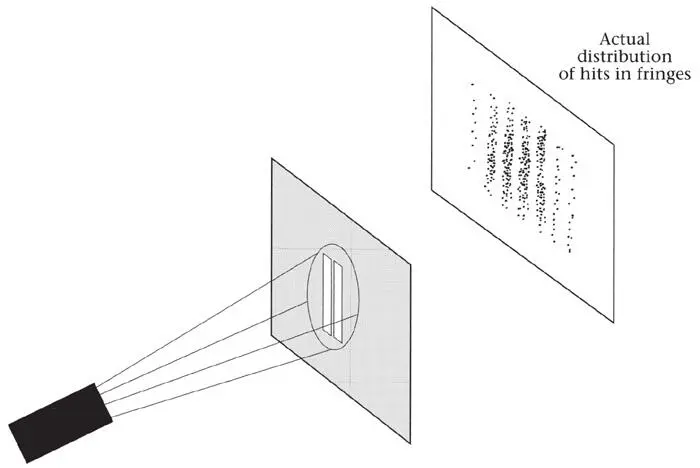
Figure 34.The actual distribution behind two slits.

Nothing remotely resembling this is observed. The hits are distributed in the bands or fringes (Figure 34) characteristic of the interference that led Young to the wave theory of light (Figure 22). When, in the nineteenth century, it was believed that these fringes are built up continuously, and not in individual ‘hits’, it seemed that only a wave field could produce them.

In the absence of a detailed theory, the pattern observed behind a single slit can be explained equally well by particles or waves. But the pattern behind two slits seems totally inexplicable on the assumption of particles. For surely a particle can pass through only one slit, and what it does then will depend solely on the properties of that slit. It cannot ‘know’ whether the other slit is open or closed and change its behaviour accordingly. Moreover, we can do similar experiments with many slits of different shapes and sizes. Invariably, wave theory correctly predicts the pattern produced on the screen. As far as the total intensity pattern is concerned, there is no way to explain it except by a wave theory.

Yet the patterns are always built up by individual ‘hits’. This is extraordinarily strong evidence for particles. But if particles are creating the patterns, they must somehow explore all the slits at once. They must do what the very concept of a particle denies – be everywhere at once. Moreover, this ability to be present at several places at once gives rise to self-interference . Dirac put it memorably: ‘Each photon ... interferes only with itself.’ It is an important observational fact that the possibility for interference to occur continues until something like the screen forces the particle ‘to reveal itself.

As long as the particle is not forced to make a choice, its behaviour in quantum mechanics is described by what Schrödinger called a wave function , which he denoted by the Greek letter psi, ψ, and this has become traditional. Sometimes the capital is used: ψ. I shall use this suitably grander capital in quantum cosmology, keeping ψ for the things that happen in laboratories. The wave function is like an intensity. If x is a point in space, ψ( x ) is the value of ψ at x . In general ψ has a different value for each x . The wave function represents something completely new in physics. A further novelty is that the wave function is not an ordinary number, as it would be for a simple intensity, but a complex number (Non-mathematicians should not get alarmed: it will be quite sufficient to think of a complex number as a pair of ordinary numbers. ‘Complex’ in this context means ‘composite’, not ‘complicated’.)

The status of the wave function is contentious to say the least. Some claim it merely represents knowledge, while others want to make it as physical as Faraday’s magnetic field. As I see things, the wave function is incorporeal (not some physical thing like a field or particle) and establishes a ranking of things. The real things are the points of Platonia, the instants of time. Quantum cosmology – at least in one embryonic form – will associate a value of ψ (note the capital) with each point of Platonia. To emphasize how different the wave function is, I like to think of it as some ‘mist’ that hangs or hovers over Platonia, its intensity varying from point to point.