Julian Barbour - The End of Time - The Next Revolution in Physics

Actually, there are two mists because the wave function, being complex, contains two numbers, which are its two components . I shall call them the red mist and green mist , respectively. I shall also introduce a third number, calling it the blue mist . The intensity of this third mist is determined by the two primary components as the sum of the squares of the red and green intensities. This is the mist mentioned in the early chapters. Those in the know will recognize the three mists as the real and imaginary parts of the wave function and the square of its amplitude.

The prominence that I give to these mists could be regarded by most theoretical physicists (above all Dirac and Heisenberg, were they still alive) as a one-sided, if not to say distorted and naive picture of quantum mechanics. The mists (as opposed to things called operators) are not particularly appropriate for talking about most quantum experiments currently performed in laboratories. However, the experiment I have in mind is not done in a laboratory. It is what the universe does to the instants of time. For this experiment, the one that really counts, I think the language of mists is appropriate. Those who disagree might have second thoughts if they really started to think of how inertial frames and duration arise. I come back to these issues later.

I shall now give, in familiar space-time terms, a quantum-mechanical account of the two-slit experiment (Figure 35). At an initial time, the wave function associated with a particle is in a ‘cloud’ well to the left of the barrier. Inside the cloud, ψ is not zero. Outside, it is zero. As time passes, this cloud moves to the right and, in general, changes its shape. It evolves (in accordance with some definite rules). Typically, it ‘spreads’. At the barrier, some of the cloud is reflected back to the left but some passes through the two slits. Initially there are two separate clouds, but they spread rapidly if the slits are narrow, and soon overlap. Characteristic wave interference occurs. Thus, when the merged wave reaches the screen, ψ is not the same everywhere, and fringes can form. In fact, the best fringes are formed by a steady ‘stream’ of wave function, not a cloud.

The question now arises: where will the particle in Figure 35 be observed? The answer, given already by the German physicist Max Born in 1926, is that ψ determines, through the intensity of the blue mist, the probability of where the particle will be observed. The blue mist enables you to guess where the particle will ‘hit’ – twice the intensity means twice the probability.

There are many mysteries in quantum mechanics, and the first is the probabilities. We can send identical clouds through the slits many times. The fringe patterns are always exactly reproduced, but the hits are distributed randomly. Only after many ‘runs’ does a pattern of hits build up. The blue mist gives that pattern. Where its intensity is high, many hits occur; where it is low, few; where it is zero, none. Quantum mechanics determines these probabilities perfectly, but says nothing about where the individual hits will occur.

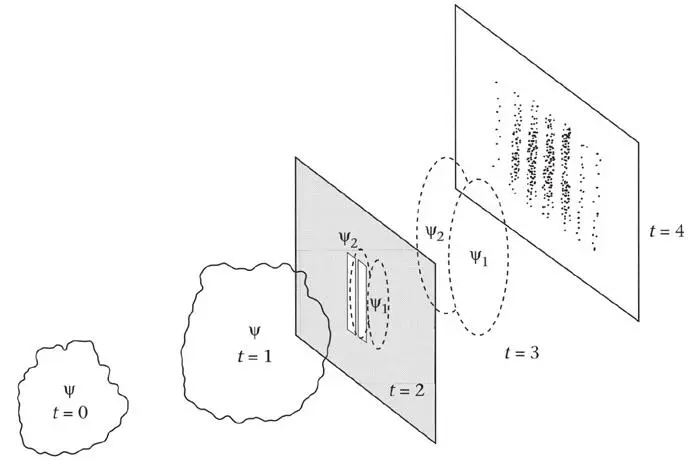
Figure 35.A ‘cloud’ of wave function ψ approaching two slits (at t = 0 and t = 1), passing through them, dividing into two (at t = 2), spreading and overlapping (t = 3) and impinging on a screen (t = 4).

Einstein found this decidedly disturbing. He could not believe that God reaches for a die every time physicists set up such an experiment and force the particle to show up somewhere. For that is what standard quantum mechanics implies – brute chance determines outcomes. But there are even more puzzling things. It is worth saying that quantum mechanics has a remarkably beautiful and self-contained structure. Examined mathematically, it is a very harmonious whole. It is hard to see how its structure could be modified naturally to make it determine where individual hits occur, especially when relativity is taken into account.

The next mystery is the collapse of the wave function . Just before the particle hits the screen, its ψ can be spread out over a large region. What happens to ψ when the particle is suddenly found somewhere? The standard answer is that the wave is instantaneously annihilated everywhere except where the particle is now known to be.

If we want to determine what now happens, we have to start afresh from a small, reduced cloud. The large cloud has been ‘collapsed’ and has no more relevance. This too provokes much puzzling, especially for those (like Schrödinger in 1926) who would wish to think of ψ as something real, a density of charge, say. How can something real disappear instantaneously? Nothing in the equations describes the collapse – it is simply postulated. Lawful evolution, in accordance with the rules (equations) of quantum mechanics, continues until an observation is made, but then the rules are simply set aside. Quite different rules apply in measurements , as they are called. (In quantum mechanics, the term ‘measurement’ is used a very precise way. It means that some definite arrangement of instruments is used to establish the value of some physical property – say the speed or position of a particle.) The abrupt and schizophrenic change of the rules when measurements are made is a major part of the notorious measurement problem . There are rules for evolution and rules for measurement – and they are even more different than chalk and cheese. Nevertheless, both are excellently confirmed, though we have to be careful when saying that the collapse is instantaneous, and even when it occurs.

Just as mysterious as the rule change when measurements are made is a certain mutual exclusivity about the kinds of measurement that can be made. So far, I have talked only about particle positions. However, we can also measure other quantities – for example, a particle’s energy, momentum or angular momentum. It is particularly fascinating that information about them all is coded at once in ψ. This is another big difference from classical mechanics.

Imagine a perfect sinusoidal wave that extends with constant wavelength from infinity to infinity. For the moment, suppose that it is ‘frozen’, like the wave patterns you see in damp sand at low tide. Let me call this the red wave, because it represents the red mist. Now imagine another identical though green wave, shifted forward by a quarter of a wavelength relative to the red wave (Figure 36). Then the red peaks lie exactly at the green wave’s nodes, where the green wave has zero intensity. As time passes, the red and green waves move to the right, maintaining always their special relative positioning. A wave function in this special form represents a particle that has a definite momentum: if it hit something, it would transmit a definite impulse to it. A particle with the opposite momentum is represented similarly, but travels in the opposite direction and has the green peaks a quarter of the wavelength behind the red peaks. According to the quantum rules, the particle has a definite momentum because its ψ has a definite wavelength and is perfectly sinusoidal. Such wave functions give the best interference effects in two-slit experiments. They are called momentum eigenstates . (The German word eigen means ‘proper’ or ‘characteristic’.)