The italics are called for. We have reached the critical point. The suggestion is that the universe as a whole is described by a single, stationary, indeed static state. Why should this – with its implication that nothing happens – be so? This is where we start to make contact with the earlier part of the book. Time and change come to an end when Machian classical dynamics meets quantum mechanics. We have seen that a Machian universe should have only one value of the energy: zero. We also know (Box 2) that a quantum theory can be obtained by quantizing a corresponding classical theory. In fact, it is easy to show that whereas quantizing Newtonian dynamics, with its external framework of space and time, leads to the time-dependent Schrödinger equation, quantizing the simple Machian model considered in Chapter 7 leads to a quantum theory in which the basic equation is not the time-dependent but the stationary Schrödinger equation.
If the Machian approach to classical dynamics is correct, quantum cosmology will have no dynamics. It will be timeless. It must also be frameless.
CREATION AND THE SCHRÖDINGER EQUATION
Before I can explain how this can be achieved, I must tell you what the Schrödinger equation is like and what it can do. I believe it is even more remarkable than physicists realize. This is where – if I am right – we are getting near the secret of creation.
When Schrödinger created wave mechanics, Bohr’s was the only existing model of the atom. It suggested that atoms could exist in stationary states, each with a fixed energy, photons being emitted when the atom jumped between them. Schrödinger’s great aim was to explain how the stationary states arise and the jumps occur. De Broglie’s proposal suggested strongly that a stationary state should be described by a wave function that oscillated rapidly in time with fixed frequency, though its amplitude might vary in space. As a first step Schrödinger therefore looked for an equation for the variation in space.
It is ironic that only later did he find the time-dependent equation from which, strictly speaking, he should have derived this equation. However, he had luck and was guided by good intuition. Although it is easy for mathematicians, I shall not go into the details of how Schrödinger found his equations or how to get from one to the other. Box 13 gives the minimum about the stationary equation needed to understand the thrust of the story.
BOX 13 How Creation Works
You can think of the Schrödinger wave function in a stationary state as follows. At each point of the configuration space Q, imagine a child swinging a ball in a vertical circle on a string of length 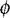 , which remains constant. As the ball whirls, its height above or below the centre of the circle changes continuously. The height is an image of the red mist, which is sometimes positive (above the centre), sometimes negative (below it). The distance sideways – to the right (positive) or the left (negative) – is an image of the green mist. The square of
, which remains constant. As the ball whirls, its height above or below the centre of the circle changes continuously. The height is an image of the red mist, which is sometimes positive (above the centre), sometimes negative (below it). The distance sideways – to the right (positive) or the left (negative) – is an image of the green mist. The square of 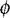 is the image of the constant intensity of the blue mist. A stationary state is like having children swinging such balls at the same rate everywhere in Q, all perfectly in phase – they all reach the top of the circle together. The only thing not perfectly uniform is the string length,
is the image of the constant intensity of the blue mist. A stationary state is like having children swinging such balls at the same rate everywhere in Q, all perfectly in phase – they all reach the top of the circle together. The only thing not perfectly uniform is the string length, 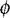 , which can change from point to point in Q. In a momentum eigenstate,
, which can change from point to point in Q. In a momentum eigenstate, 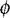 is the same everywhere. It is a very special state, but in a more general stationary state
is the same everywhere. It is a very special state, but in a more general stationary state 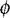 does vary over Q. The stationary Schrödinger equation governs its variation.
does vary over Q. The stationary Schrödinger equation governs its variation.
It does this by imposing a condition at each point of Q. The sum of two numbers, calculated in definite ways, must equal a third. The first number is the most interesting but the most difficult to find. Take a quantum system of three bodies. Its configuration space Q has nine dimensions. Each point in Q corresponds to a position of the three bodies in absolute space. Imagine holding two bodies fixed, and moving the third along a line in absolute space. This will move you along a line in Q. Suppose that along it you plot 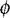 , the string length, as a curve above the line. At each point, this curve will have a certain curvature. At some places it will curve strongly, towards or away from the line, at others weakly. In the calculus, the curvature is the second derivative.
, the string length, as a curve above the line. At each point, this curve will have a certain curvature. At some places it will curve strongly, towards or away from the line, at others weakly. In the calculus, the curvature is the second derivative.
At each point of Q there are nine such curvatures because Q has nine dimensions, one for each of the three directions in absolute space in which each particle can move. The first number in the Schrödinger condition is the sum of these nine curvatures after each has been multiplied by the mass of the particle for which it has been calculated. I shall call this the curvature number .
The second number is much easier to find. Recall that any configuration of bodies has an associated potential energy. The configuration (and the nature of the bodies, their masses, etc.) determines it uniquely. For gravity, this was explained in Figure 17. The second number, which I shall call the potential number , is found simply by multiplying the potential by 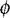
The third number is also easy to find. If ω is the frequency of the state (the number of ‘rotations of the balls’ in a second), then, by the quantum rules, the energy of the state is E = hω , where h is Planck’s constant. This is the relationship Einstein found between the energy and frequency of a photon. The third number, which I shall call the energy number , is then found by multiplying the energy E by 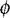 .
.
The condition imposed by the stationary Schrödinger equation is then
Curvature number + Potential number = Energy number
(Planck’s constant also occurs in the first number, to ensure that all three numbers have the same physical nature.)
However, finding this condition, which must hold everywhere in Q, was only half the story. Schrödinger thought that an atom in a stationary state was like a violin string vibrating in resonance. Because its two ends are fixed, the amplitude at the ends is zero. He therefore imposed on 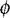 not only the above condition, but also the condition that it should tend to zero at large distances. It was this requirement that enabled him to make the huge discovery that convinced him – and very soon everyone else – that he had found the secret of Bohr’s quantum prescriptions.
not only the above condition, but also the condition that it should tend to zero at large distances. It was this requirement that enabled him to make the huge discovery that convinced him – and very soon everyone else – that he had found the secret of Bohr’s quantum prescriptions.
This hinges on an extremely interesting property of the stationary Schrödinger equation. As yet E is a fixed but unknown number. It may be smaller or greater than the potential V , which varies over Q . The interesting thing is that the above condition forces 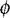 to do very different things depending on the value of E – V . Where it is greater than zero,
to do very different things depending on the value of E – V . Where it is greater than zero, 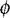 oscillates. As Schrödinger said rather quaintly, ‘it does not get out of control’. However, where E – V is less than zero, the condition forces an entirely different behaviour on
oscillates. As Schrödinger said rather quaintly, ‘it does not get out of control’. However, where E – V is less than zero, the condition forces an entirely different behaviour on 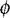 . It must either tend rapidly to zero or else grow rapidly – exponentially in fact – to infinity. The latter would be a disaster. Schrödinger therefore commented that things become tricky and must be handled delicately. Indeed, he showed that it is only in exceptional cases, for special values of E , that
. It must either tend rapidly to zero or else grow rapidly – exponentially in fact – to infinity. The latter would be a disaster. Schrödinger therefore commented that things become tricky and must be handled delicately. Indeed, he showed that it is only in exceptional cases, for special values of E , that 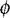 does not ‘explode’ but instead subsides to zero at infinity. These are the cases he was looking for. Well-behaved solutions exist for only certain values of E , which are discrete (separated from each other) if E is less than zero.
does not ‘explode’ but instead subsides to zero at infinity. These are the cases he was looking for. Well-behaved solutions exist for only certain values of E , which are discrete (separated from each other) if E is less than zero.
Читать дальше

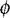 , which remains constant. As the ball whirls, its height above or below the centre of the circle changes continuously. The height is an image of the red mist, which is sometimes positive (above the centre), sometimes negative (below it). The distance sideways – to the right (positive) or the left (negative) – is an image of the green mist. The square of
, which remains constant. As the ball whirls, its height above or below the centre of the circle changes continuously. The height is an image of the red mist, which is sometimes positive (above the centre), sometimes negative (below it). The distance sideways – to the right (positive) or the left (negative) – is an image of the green mist. The square of 










