The well-behaved solutions are called eigenfunctions , and the corresponding values of E are called (energy) eigenvalues . It is a fundamental property of quantum mechanics that any system always has at least one eigenfunction. The eigenfunction of any system that has the lowest value of its energy eigenvalue (there is often only one such eigenfunction) is called the ground state . In general, there are also eigenfunctions with higher energies, called excited states . Finally, if E is large enough for E – V to be positive everywhere, the eigenfunctions oscillate everywhere, though more rapidly where the potential is lowest. The negative eigenvalues E form the discrete spectrum , and the corresponding states are called bound states because for them 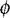 has an appreciable value only over a finite region. The remaining states, with E greater than zero, are called unbound states , and their energy eigenvalues form the continuum spectrum .
has an appreciable value only over a finite region. The remaining states, with E greater than zero, are called unbound states , and their energy eigenvalues form the continuum spectrum .
Schrödinger won the 1933 Nobel Prize for Physics mainly for his wave-mechanical calculation for the hydrogen atom. He found that the energy eigenvalues of its stationary states are precisely the energies of the allowed states in Bohr’s model. This was a huge advance, since Schrödinger’s formalism had an inner unity and consistency to it completely lacking in the older model. Brilliant successes of the new wave mechanics, many achieved by Schrödinger himself, soon came flooding in, leaving no doubt about the great fruitfulness of the new scheme.
In Chapter 14 I described how molecules appear in the Schrödinger picture: as immense collections of all the configurations they could conceivably have, with the blue mist of the quantum probability strongly concentrated on the most probable configurations. These most probable configurations, generally clustered around a single point in Q, are the ones represented by the ball-and-strut models. I can now begin to make good my claim that Schrödinger found the laws of creation. His stationary equation determines the structures – indeed, creates the structures – of all these amazing atoms and molecules that constitute so much of the matter in the universe, our own bodies included. The equation does it by determining which structures are probable. But I mean creation not only in this sense of the structure of atoms and molecules, but in an even deeper one. The full explanation is still to come, but we are getting closer to our quarry.
QUANTUM MECHANICS HOVERING IN NOTHING
We must now see if we can dispense not only with time but also with absolute space in quantum mechanics. In a timeless system the energy E is zero, and the condition in Box 13 says simply that at every point of Q the sum of the curvature number and the potential number is zero. The potential number is already in the form we need. For any possible relative configuration, the potential has a unique value: it depends on nothing else. To find the potential number, we simply calculate the potential V for each configuration and then multiply by 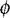 , getting
, getting 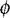 This part of the calculations is pleasingly self-contained because V depends only on the relative configuration. Each structure has its own potential irrespective of how we imagine the structure to be embedded in space.
This part of the calculations is pleasingly self-contained because V depends only on the relative configuration. Each structure has its own potential irrespective of how we imagine the structure to be embedded in space.
However, a lack of ‘self-containment’ shows up in the curvature number. To find it, we must know how 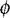 varies from position to position in the configuration space Q. This is not a self-contained process in Schrödinger’s equation because the points of his Q are defined by the particles’ positions in absolute space, which is used crucially in Q, making it hybrid . The all-important curvatures of
varies from position to position in the configuration space Q. This is not a self-contained process in Schrödinger’s equation because the points of his Q are defined by the particles’ positions in absolute space, which is used crucially in Q, making it hybrid . The all-important curvatures of 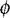 are ultimately determined by position differences in absolute space. As a result, in standard quantum mechanics the orientations are in general entangled with the relative data that specify the particle separations. Now, besides positions, momenta and energy there is another very important quantity in quantum mechanics – angular momentum, which, being an action, always has discrete eigenvalues. It owes its existence in quantum mechanics to absolute space. We have not yet escaped from Newton’s framework.
are ultimately determined by position differences in absolute space. As a result, in standard quantum mechanics the orientations are in general entangled with the relative data that specify the particle separations. Now, besides positions, momenta and energy there is another very important quantity in quantum mechanics – angular momentum, which, being an action, always has discrete eigenvalues. It owes its existence in quantum mechanics to absolute space. We have not yet escaped from Newton’s framework.
We are now coming to another critical point. We have seen that in classical physics the action is a kind of ‘distance’ between two configurations that are nearly but not exactly the same. Absolute space is an auxiliary device that makes it possible to define such ‘distances’. This is why angular momentum exists in classical and quantum physics. However, in Chapter 7 we found an alternative definition of ‘distances’ that works in the purely relative configuration space – in Platonia – and owes nothing to absolute space. They are defined by the best-matching procedure, which uses relative configurations and nothing else. In classical physics, this makes it possible to create a purely relative and hence self-contained dynamics. We also found that a sophisticated form of best matching lies at the heart of general relativity. Best matching would appear to be a basic rule of the world.
It is therefore very tempting to see whether it can be applied in quantum mechanics. What we would like to do is establish rules for operating on wave functions defined solely on the relative configuration space. For example, for three bodies we would want to eliminate the six dimensions associated with their position and orientation in absolute space, and work just with the sides of the triangle. We shall then have a wave function defined on a three-dimensional Platonia. For that, we shall want to calculate a curvature number and a potential number. The latter will present no difficulty, since it will be the same as in ordinary quantum mechanics. The difficulty is in the curvature number. What, after all, is curvature? For any given curve, it is the rate at which its slope changes. But the key thing about a rate of change is that it is with respect to something . That something is all-important. It is a kind of ‘distance’. The ordinary quantum-mechanical ‘distance’ is simply distance in absolute space (times the mass of the particle considered). To eliminate absolute space in classical physics, we replaced it by the Machian best-matching distance. There is no reason why we should not do the same in quantum physics.
This is where the unfolding of quantum mechanics on configuration space is so important. To retain that essential property of it – the huge step that Schrödinger took – we must pass from his hybrid Q to Platonia. If we are to succeed in formulating quantum mechanics in the new arena, there must be ‘distances’ in it. But that is precisely what the best-matching idea was developed to provide. Exactly the same ‘distances’ needed to realize Mach’s principle in classical physics can be used in a version of wave mechanics for a universe without absolute space. All we have to do is measure curvatures with respect to the Machian distances created on Platonia by best matching. We then add curvatures measured in as many mutually perpendicular directions as there are dimensions in that timeless arena, and set the sum equal to minus the potential number.
In fact, it is quite easy to see that the wave functions that satisfy the Schrödinger conditions in this Machian case are precisely the eigenfunctions of ordinary quantum mechanics for which the angular-momentum eigenvalues are zero. This exactly matches our result in classical mechanics – that the best-matching condition leads to solutions identical to the Newtonian solutions with angular momentum zero. We have already seen why they must be static solutions.
Читать дальше

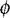 has an appreciable value only over a finite region. The remaining states, with E greater than zero, are called unbound states , and their energy eigenvalues form the continuum spectrum .
has an appreciable value only over a finite region. The remaining states, with E greater than zero, are called unbound states , and their energy eigenvalues form the continuum spectrum .










