Julian Barbour - The End of Time - The Next Revolution in Physics

I begin by looking at the special theory of relativity, in which gravity plays no role. I then go on to the general theory, in which Einstein found a most brilliantly original way to describe gravity. In both relativity theories time seems to be very real and to behave in baffling ways. But, as became clear only after Einstein’s death, his theory has a deep structure which is revealed only by an analysis of how it works as a dynamical theory. It is this deep structure that is timeless. Quite a large proportion of Part 3 will explain the purely historical accidents that obscured the deep structure of general relativity for so long.

In the whole of physics, nothing is more remarkable than the transformation wrought by a simple question that Einstein posed in 1905: what is the basis for saying that two events are simultaneous? Einstein was not the first to ask it. James Thomson, brother of Lord Kelvin, had in 1883. More significantly, so had Poincaré – a great figure in science – in 1898, in a paper that Abraham Pais, Einstein’s biographer, calls ‘utterly remarkable’. In connection with historical accidents, Poincaré’s paper is very interesting. He identified two problems in the definition of time.

First he considered duration: what does it mean to say that a second today is the same as a second tomorrow? He noted that this question had recently been widely discussed, and he outlined the astronomers’ solution, the ephemeris time described in Chapter 6. However, he then noted a second question, just as fundamental and in some ways more immediate, which had escaped close attention. How does one define simultaneity at spatially separated points? This was the question that Einstein posed and answered seven years later with such devastating effect. I read the subsequent history of relativity as follows. Einstein answered his question – Poincaré’s second – with such aplomb and originality that it eclipsed interest in the question of duration. It is not that duration plays no role in relativity – quite the opposite, it plays a central role. But duration is not derived from first principles. It appears indirectly.

One of the main aims of Part 3 is to redress the balance, to treat duration at the same level as simultaneity. There is, in fact, a beautiful theory of duration at the heart of general relativity, but it is hidden away in sophisticated mathematics. Einstein had no inkling of this. He said of his own theory that no one who had grasped its content could ‘escape its magic’. But the magic was more potent than even he realized. It can, it almost certainly will, destroy time.

Much of nineteenth-century physics can be seen as meticulous preparation for the denouement over simultaneity. It had to come, but what a coup de théâtre Einstein made of it. Many readers will be familiar with the story, but since it introduces important ideas I shall briefly recall some key elements. It all started with an investigation of interference carried out in 1802 by the English polymath Thomas Young, famous among other things for his decipherment of the Egyptian hieroglyphs on the Rosetta Stone. In a sense, this was the start of both relativity and quantum theory. Young observed that if light from a single source is split into two beams that are subsequently recombined and projected onto a screen, then bright and dark fringes appear. He interpreted them in terms of a wave theory of light. If light is some kind of wave motion, there will be wave crests and troughs in both beams. When they are recombined, there will be places where the crests from one beam coincide with troughs in the other. They will cancel, giving dark fringes. But where crests coincide, they will enhance each other, giving bright fringes (Figure 22). Innumerable natural phenomena are explained by interference.

Young’s insight, which was developed more or less independently and much more thoroughly some years later by the Frenchman Augustin Jean Fresnel, soon gave rise to the notion that light waves must be vibrations of some elastic medium, which was called the aether . Meanwhile, the study of electricity and magnetism developed rapidly. In 1831, the English scientist Michael Faraday discovered electromagnetic induction, which not only showed that electricity and magnetism were related phenomena but rapidly became the basis of all electrical machinery. Deeply impressed by the patterns formed by iron filings sprinkled on paper held near a magnet (Figure 23), Faraday introduced the notion of lines of force and fields . A field can be thought of as a tension or excitation that exists throughout space and varies continuously (as demonstrated by induction) in both space and time. The field concept eventually changed physicists’ picture of what the world is ‘made of.

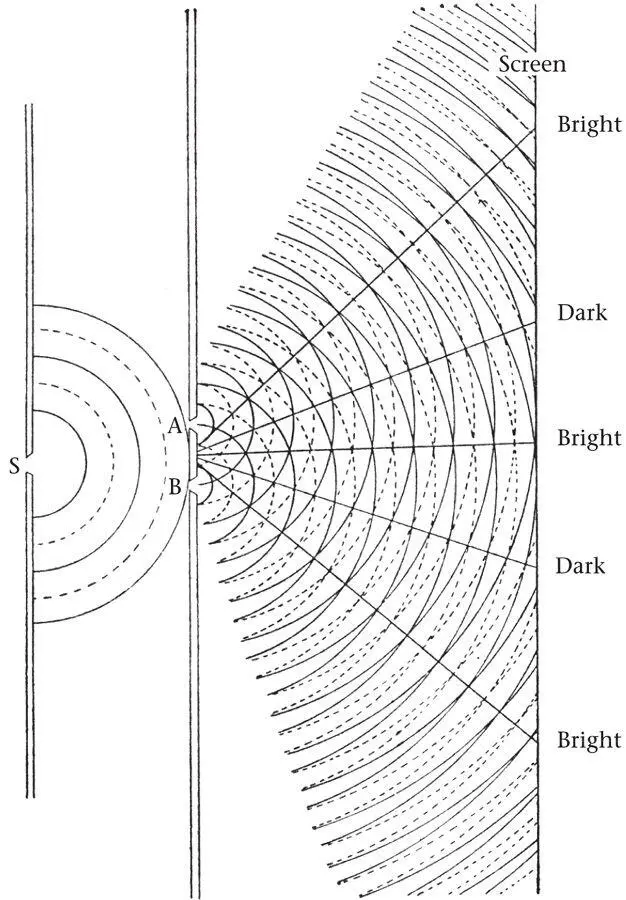
Figure 22.Thomas Young’s original explanation of the interference fringes in accordance with the wave theory of light, which he deduced by analogy with the behaviour of water waves. According to this interpretation, the beam reaches the barrier in the form of a plane wave, the successive parallel crests of which arrive simultaneously at the two slits A and B. The wave is diffracted at each slit, and spherical waves spread out from each point of the two slits towards the screen. At some points on the screen, the wave crests (or troughs) from the two slits arrive simultaneously, and the wave intensity is enhanced (bright regions). At other points, a wave crest from one slit arrives with a wave trough from the other. The wave intensity is cancelled at such a point (dark regions). This is the classical explanation of the fringes in terms of interference.

In the decade from 1855, the Scottish physicist James Clerk Maxwell took up Faraday’s qualitative field notion and cast it into mathematical form. His equations showed that electromagnetic effects should propagate through empty space as waves with a speed determined by the ratio of certain constants. It had already been noted that the ratio was equal to the known speed of light, leading to the strong suspicion that light was an electromagnetic effect. Maxwell’s equations proved this. Electromagnetic effects can propagate as waves of many different wavelengths: from radio waves (with wavelengths of around a metre to a kilometre), microwaves (wavelengths measured in centimetres), infrared waves (some ten to a thousand waves per centimetre), visible light (roughly ten thousand waves to the centimetre), ultraviolet light (up to around a million waves per centimetre), X-rays (of the order of ten million waves in every centimetre) and gamma rays (billions or even trillions of waves per centimetre). Hertz’s celebrated detection of waves from an electromagnetic source in 1888 was the first confirmation of this consequence of Maxwell’s theory.

Figure 23.Magnetic lines of force as revealed by placing iron filings in the magnetic field of a bar magnet.

Virtually all physicists were convinced that these electromagnetic excitations must be carried by some mechanical aether. This put a remarkable twist into the theory of motion and the status of Newton’s absolute space. Even in the framework of Newtonian theory, there had always been one serious problem with the notion. Newton was not entirely frank about it. In his guts, he certainly believed in a state of absolute rest. When he introduced absolute space, his words suggested the existence of one unique framework of motion. Either you moved with respect to it or you did not. However, in the body of the Principia he stated and used correctly the relativity principle, according to which the motions within a system are completely unaffected by any uniform overall motion it has (Box 5). This seriously undermined the idea of a unique state of rest – no criterion could establish whether one were in it or moving uniformly.