Julian Barbour - The End of Time - The Next Revolution in Physics

The magical touch was that his choice was the most natural thing to do – in the theory of an aether and in the context of the relativity principle. Given their apparent irreconcilability, his subsequent demonstration of their compatibility was a coup. It also showed that there was something inevitable about the result.

For suppose there is a pond-like aether and that nothing is faster than light. It is natural to assume that it travels equally fast in all directions. Then how are we to define simultaneity throughout the aether? Einstein proposed setting up a master clock at a central reference point, sending a light signal to some distant identical clock at rest relative to it, and letting the signal be reflected back to the master clock. If it measures a time T for the round trip, we would obviously say that the light took ½T to reach the distant clock, which can be synchronized to read t + ½T on the arrival of a signal sent by the master clock when it reads t . In this way, clocks throughout the aether can be synchronized with the master clock. Standard measuring rods can be used to measure the distances between them. This is the obvious way to set up a space-time grid if the aether theory is correct.

However, it does assume that the aether is ‘visible’ and that we know when we are at rest in it. But this the relativity principle denies. Imagine a family of observers, equipped with clocks to measure time and rods to measure length, distributed in space and at rest relative to one another. Believing themselves at rest in the aether, they define simultaneity by Einstein’s prescription. There is also a second family, with identical rods and clocks, also at rest relative to one another but moving uniformly relative to the first. By the relativity principle, they can equally believe themselves at rest in the aether. So they too will use Einstein’s prescription to define simultaneity. Just as belief in the aether theory makes the prescription natural, belief in the relativity principle makes it natural for both families to adopt it. Nothing in nature privileges one family over the other. Whatever one family does, the other can do with equal right. In particular, each can use Einstein’s prescription.

The inescapable consequence is that the two families will disagree about which events are simultaneous. However, by accepting this, Einstein achieved his first goal – the demonstration that light propagation takes an identical form for both families (Box 9). This remarkable fact – that the relativity principle holds for light propagation and that simultaneity depends on the observer and on convention – is thus the great denouement towards which so much wonderful physics in the nineteenth century had been tending. It also showed that the aether is a redundant concept, since no experiment can establish whether we are moving relative to it.

Lack of simultaneity was only the beginning. Einstein went on to draw further amazing consequences from his iron insistence that all phenomena must unfold in exactly the same way for any two families of observers in uniform motion relative to each other. In particular, he was able to make some startling predictions about rods and clocks. The point is that the facts of light propagation are established by means of physical rods and clocks, but these tools are not immune to the relativity principle. Using simple equations and precise arguments, Einstein showed that two such families must each come to the conclusion that the clocks of the other family, moving relative to them, run slower than their own clocks. Each family also concludes that the rods of the other family are shorter than their own.

What is so remarkable about these results – and it seems so impossible that many quite intelligent people still refuse to accept it – is their mutual nature. How can it be that each family finds that the clocks of the other family run slower than their own? Box 10 explains.

BOX 9 Relativity in One Diagram and 211 Words

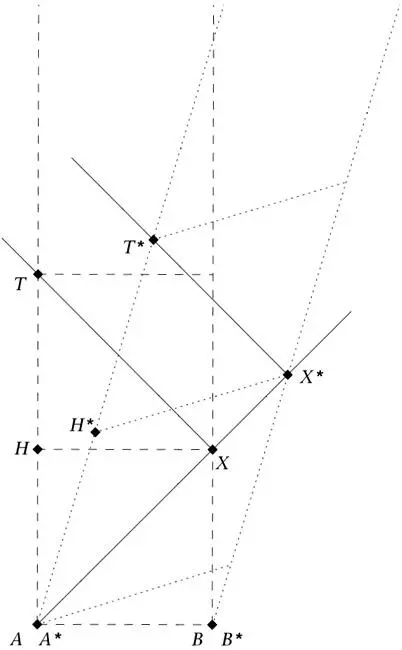
Figure 25.Alice (A) and Bob (B) believe they are at rest in the aether, and therefore draw a grid (dashes) with time vertical and space (only one dimension shown) horizontal. To synchronize their clocks, Alice sends Bob a light signal (solid line), which reaches him at X, where it is reflected back to Alice at T. Alice concludes that the signal reached Bob when she was at H. Their identical twins Alice* (A*) and Bob* (B*) are moving uniformly relative to them, but also believe they are at rest. Alice* sends a light signal, just as her twin does, at the moment they meet. It reaches Bob* at X*, and the reflection of it returns to Alice* at T*. She therefore concludes that her signal reached Bob* at H*, so she and Bob* have a grid (dots) inclined relative to their twins’ grid. The pairs do not agree on which events are simultaneous. Alice and Bob think H and X are, their twins think H* and X* are. However, they confirm the relativity principle, since both find that light travels along rays parallel to the diagonals (AX, XT and A*X*, X*T*) of their respective coordinate grids. Despite appearances, the situation is symmetric – in Alice* and Bob*’s grid their twins’ grid appears skew.

Fascinating as the results of Einstein’s two relativity theories are, many of them are not directly relevant to my main theme. Popular accounts that cover topics I omit are recommended in the section on Further Reading. My aim in Part 3 is to show how Einstein’s approach to relativity led him to an explicit theory of simultaneity but an implicit theory of duration. It is the latter that is important for this book, but it never got properly treated in relativity. The point is that remarkable facts about duration, as revealed through the clocks of different observers, follow inescapably from the definition of simultaneity and the relativity principle. Einstein did not need to create a theory of clocks and duration from first principles in order to learn some facts about them: they already followed from his two primary postulates.

BOX 10 The Impossible Becomes Possible

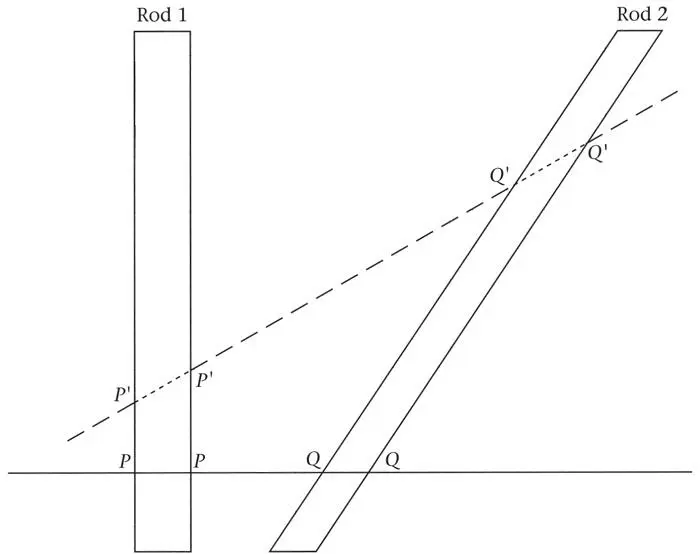
Figure 26.The horizontal and inclined strips, in which time increases vertically and the horizontal represents one space dimension, show the histories of two physically identical rods moving uniformly relative to each other. For Bob and Alice, points on the continuous line PPQQ are simultaneous and show the positions and lengths of the rods at the corresponding times. Their rod, PP, appears longer than Bob* and Alice*’s rod, QQ. But the starred twins think that points on the line P’P’Q’Q’ are simultaneous, and conclude that their rod Q’Q’ is longer than P’P’. A similar illustration could be given for clocks. Such diagrams do not explain this behaviour of rods and clocks, but do show that there is no outright logical contradiction. Einstein’s conclusions are as secure as his premises. His confidence in them has so far been totally vindicated.

The method Einstein used to create his relativity theories is an important factor. During the nineteenth century, mainly through the development of thermodynamics, physicists began to distinguish between, on the one hand, theories of the world in terms of truly basic laws and constituents (e.g. atoms and fields) and, on the other hand, so-called principle theories. In the latter, no attempt would be made to give an ultimate theory of things. Instead, the idea was to seek principles that seemed to hold with great generality and include them in the foundations of the description of phenomena. The repeated failures of all attempts to build perpetual-motion machines, of which two distinct types could be envisaged, became the basis of the first and second laws of thermodynamics. In the form in which it was developed on this basis, thermodynamics was a theory of the second kind – a principle theory.