31 Ясно, что то, что Архит называет математикой и что мы некритично также считаем просто математикой, отнюдь ею не было.
32 МД, III, 55, В1.
33 Платон. Филеб, 17е, 3 (1), (19).
34 «Пифагорейская теория музыки, как и все одновременно с ней возникшие физические теории (атомизм представляет типический пример), выросла не на почве точных экспериментов». Б. Л. Ван дер Варден. Цит. соч., с. 410.
35 См., например, И. Г. Башмакова. Лекции по истории математики в древней Греции.— «Историко-математические исследования, вып. XI. М., 1958, с. 245. Э. Кольман. История математики в древности. М., 1961, с. 83.
36 A . Szabo . Op . cit ., S . 224. На генетическую связь пифагорейской аритмологии с музыкальной теорией и практикой, с опытными исследованиями акустического консонанса указывали ранее П. Таннери и О. Веккер. См .: P. Tannery. Du role de la musique grecque dans le development de la mathernatique pure.— In: Memoire scientifique. Bd III. Toulouse — Paris, 1912, p. 68—69; 83—89; 0. Becker. Zur Geschichte der griechischen Mathematik! Darmstadt, 1965, S. 143.
37 A. Seidenberg. The Ritual Origin of Geometry.— «Archive for history of exaGt sciences)), 1962, vol. 1, N 5, p. 488.
38 A. Tayler. Forms and Numbers.— «Mind», vol. 35, 1924, p. 412; vol. 36, 1927 p. 12.
39 «Принципиально не может быть у греков такой философии, которая не была бы эстетикой, и такой эстетики, которая не была бы в то же время философией и именно «первой философией». А. Ф. Лосев. Очерки античного символизма и мифологии. М., 1930, с. 84—85.
40 МД, III, 16, В2.
41 Исследование «Дорифора», в котором прослежены мельчайшие и детальнейшие пропорции его, проведено А. Калькманом. A. Kalkman. Die Proportionen des Gesichts in der griechischen Kunst. Berlin , 1893, S . 36—37.
42 Античная музыкальная эстетика. Вступительный очерк и собрание текстов проф. А. Ф. Лосева. М., 1960, с. 22.
43 Евклид. Начала, кн. VII, опр. 1. Цит. по: Начала Евклида. Пер. и комментарии Д. Д. Мордухай-Болтовского при редакционном участии И. H . Веселовского. М., 1949, кн. VII—X, с. 9. По поводу перевода этого известного определения см.: Е. М. Bruins . Printing and reprinting of theories contrary to facts and texts.— «Janus». Revue Internationale de l'histoire des sciences, de la medicine, de la pharmacie et de la technique. Brill/Leiden, 1970, LVIl, N 2—3, p. 134—149. Уточнение, которое вносится Брейнсом в перевод, сужает общность определения, но не меняет его смысла.
44 В.Л. Ван дер Варден. Цит. соч., с. 162.
45 Можно привести в этой связи следующее высказывание Галена по поводу поликлетова «Канона»: «Получить без труда навык узнавать центр 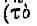
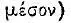 в каждом роде живых существ и во всем существующем не является делом кого попало, но — такого человека, который крайне трудолюбив и который может находить этот центр при помощи длительного опыта и многократного познавания всех частностей». Цит. по кн.: А. Ф. Лосев. История античной эстетики, с. 306.
в каждом роде живых существ и во всем существующем не является делом кого попало, но — такого человека, который крайне трудолюбив и который может находить этот центр при помощи длительного опыта и многократного познавания всех частностей». Цит. по кн.: А. Ф. Лосев. История античной эстетики, с. 306.
46 «Древность не имела никакого знакового языка, но вспомогательное средство для того, чтобы сделать наглядной как эту, так и другие операции, имела в геометрическом изображении и трактовке общих величин и тех операций, которые следовало с ними предпринимать. Н . Zeuthen. Die Lehre von der Kegelschnitten im Altertum. Kopenhagen, 1886, S. 6.
47 А. Ф. Лосев. Цит. соч., с. 307.
48 И. Н. Веселовский в предисловии к сочинениям Архимеда и в комментариях к книге Ван дер Вардена отмечает наличие как бы двух направлений в первоначальной греческой математике. Они обнаруживаются в том, что в книге I «Начал» употребляется два типа равенства. В одном случае равными считаются фигуры, совпадающие при наложении (конгруэнтные), в другом — равновеликие. Первый тип равенства характерен для традиции «ионийской математики» (доказательство посредством сгибания фигуры и наложения ее частей друг на друга) и связан, по мнению Веселовского, с вавилонским научным наследием. Второе — более свойственно италийской, пифагорейской школе и генетически связано с египетской «модулярной» математикой. Веселовский замечает, что Самос, родина Пифагора и первоначальный центр пифагорейской школы, был центром инженерии, архитектуры и скульптуры и теснейшим образом связан с Египтом. Именно здесь два скульптора сделали в разных местах две половины статуи так, что они точно подошли друг к другу. Наконец, идея всепорождающей единицы и исследование целочисленных пропорций также соответствуют, по Веселовскому, модулярному подходу. Напротив, как считает историк, геометрические построения при помощи циркуля были введены ионийскими учеными, если не Фалесом, то Энопидом Хиосским (См.: Б. Л. Ван дер Варден. Цит. соч., с. 445; Архимед. Сочинения. Предисловие, с. 18—19).
Мы должны заметить, что доступные нам и просмотренные нами материалы не могут быть приведены в согласие с концепцией И. H . Веселовского. Во-первых, как мы надеемся показать, как раз для пифагорейства середины V в. до н. э. не свойствен тот своеобразный математический атомизм, о котором говорит исследователь. Напротив, проблема иррациональности постоянно находилась в их поле зрения. Во-вторых, только длительная арифметическая практика уже в своей геометро-алгебраической форме может привести к выработке идеи некоторой абстрактной общей единицы, которую и следует поэтому искать в развитом геометризме, не свойственном пифагорейству V в. до н. э. Наконец, модулярность египетской техники в корне противоречит антропоморфизму и пластическому воззрению классической Греции, что в особенности подчеркивает А. Ф. Лосев в «Истории античной эстетики», с. 307.
Читать дальше

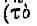
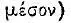 в каждом роде живых существ и во всем существующем не является делом кого попало, но — такого человека, который крайне трудолюбив и который может находить этот центр при помощи длительного опыта и многократного познавания всех частностей». Цит. по кн.: А. Ф. Лосев. История античной эстетики, с. 306.
в каждом роде живых существ и во всем существующем не является делом кого попало, но — такого человека, который крайне трудолюбив и который может находить этот центр при помощи длительного опыта и многократного познавания всех частностей». Цит. по кн.: А. Ф. Лосев. История античной эстетики, с. 306.










